About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 108 results for "P W Heijnen" clear search
Human-in-the-loop Experiment of the Strategic Coalition Formation using the glove game
Andrew Collins | Published Monday, November 23, 2020 | Last modified Wednesday, June 22, 2022The purpose of the model is to collect information on human decision-making in the context of coalition formation games. The model uses a human-in-the-loop approach, and a single human is involved in each trial. All other agents are controlled by the ABMSCORE algorithm (Vernon-Bido and Collins 2020), which is an extension of the algorithm created by Collins and Frydenlund (2018). The glove game, a standard cooperative game, is used as the model scenario.
The intent of the game is to collection information on the human players behavior and how that compares to the computerized agents behavior. The final coalition structure of the game is compared to an ideal output (the core of the games).
COMM-PDND: Communication-Based Model of Perceived Descriptive Norm Dynamics in Digital Networks
Lars Reinelt | Published Friday, September 08, 2023The Communication-Based Model of Perceived Descriptive Norm Dynamics in Digital Networks (COMM-PDND) is an agent-based model specifically created to examine the dynamics of perceived descriptive norms in the context of digital network structures. The model, developed as part of a master’s thesis titled “The Dynamics of Perceived Descriptive Norms in Digital Network Publics: An Agent-Based Simulation,” emphasizes the critical role of communication processes in norm formation. It focuses on the role of communicative interactions in shaping perceived descriptive norms.
The COMM-PDND is tuned to explore the effects of normative deviance in digital social networks. It provides functionalities for manipulating agents according to their network position, and has a versatile set of customizable parameters, making it adaptable to a wide range of research contexts.
We construct a new type of agent-based model (ABM) that can simultaneously simulate land-use changes at multiple distant places (namely TeleABM, telecoupled agent-based model). We use soybean trade between Brazil and China as an example, where Brazil is the sending system and China is the receiving system because they are the world’s largest soybean exporter and importer respectively. We select one representative county in each country to calibrate and validate the model with spatio-temporal analysis of historical land-use changes and the empirical analysis of household survey data. The whole model is programmed on RePast Simphony. The most unique features of TeleABM are that it can simulate a telecoupled system and the flows between sending and receiving systems in this telecoupled system.
Development of coral reefs under climate change impacts and adaptation options
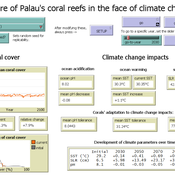
Nina Preußler | Published Friday, May 30, 2025This NetLogo model simulates how coral reefs around the islands of Palau would develop under different emission scenarios and with selected adaptation strategies. Reef health is indicated by coral cover (%) and is affected by four major climate change impacts: increasing sea surface temperature, sea level rise, ocean acidification, and more intense typhoons. The model differentiates between inner and outer reefs, with the former naturally adapted to warmer, more acidic waters. The simulation includes bleaching events and possible recovery. In addition, the user can choose between different coral transplantation strategies as well as regulate natural thermal adaptation rates.
Gender differentiation model
Sylvie Huet | Published Monday, April 20, 2020 | Last modified Thursday, April 23, 2020This is a gender differentiation model in terms of reputations, prestige and self-esteem (presented in the paper https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0236840). The model is based on the influence function of the Leviathan model (Deffuant, Carletti, Huet 2013 and Huet and Deffuant 2017) considering two groups.
This agent-based model studies how inequalities can be explained by the difference of open-mindness between two groups of interacting agents. We consider agents having an opinion/esteem about each other and about themselves. During dyadic meetings, agents change their respective opinion about each other and possibly about other agents they gossip about, with a noisy perception of the opinions of their interlocutor. Highly valued agents are more influential in such encounters. We study an heterogeneous population of two different groups: one more open to influence of others, taking less into account their perceived difference of esteem, called L; a second one less prone to it, called S, who designed the credibility they give to others strongly based on how higher or lower valued than themselves they perceive them.
We show that a mixed population always turns in favor to some agents belonging to the group of less open-minded agents S, and harms the other group: (1) the average group self-opinion or reputation of S is always better than the one of L; (2) the higher rank in terms of reputation are more frequently occupied by the S agents while the L agents occupy more the bottom rank; (3) the properties of the dynamics of differentiation between the two groups are similar to the properties of the glass ceiling effect proposed by Cotter et al (2001).
Prisoner's Tournament
Kristin Crouse | Published Wednesday, November 06, 2019 | Last modified Wednesday, December 15, 2021This model replicates the Axelrod prisoner’s dilemma tournaments. The model takes as input a file of strategies and pits them against each other to see who achieves the best payoff in the end. Change the payoff structure to see how it changes the tournament outcome!
Social model of a Team Developing a Planning-Methodology
Oswaldo Terán Christophe Sibertin | Published Monday, November 18, 2013 | Last modified Sunday, November 16, 2014The model represents a team intended at designing a methodology for Institutional Planning. Included in ICAART’14 to exemplify how emotions can be identified in SocLab; and in ESSA’14 to show the Efficiency of Organizational Withdrawal vs Commitment.
LogoClim: WorldClim in NetLogo
Daniel Vartanian Leandro Garcia Aline Martins de Carvalho Aline | Published Thursday, July 03, 2025 | Last modified Tuesday, September 16, 2025LogoClim is a NetLogo model for simulating and visualizing global climate conditions. It allows researchers to integrate high-resolution climate data into agent-based models, supporting reproducible research in ecology, agriculture, environmental sciences, and other fields that rely on climate data.
The model utilizes raster data to represent climate variables such as temperature and precipitation over time. It incorporates historical data (1951-2024) and future climate projections (2021-2100) derived from global climate models under various Shared Socioeconomic Pathways (SSPs, O’Neill et al., 2017). All climate inputs come from WorldClim 2.1, a widely used source of high-resolution, interpolated climate datasets based on weather station observations worldwide (Fick & Hijmans, 2017).
LogoClim follows the FAIR Principles for Research Software (Barker et al., 2022) and is openly available on the CoMSES Network and GitHub. See the Logônia model for an example of its integration into a full NetLogo simulation.
Peer reviewed E³-MAN. An Institutionally-guided multi-agent. Model for fair and efficient negotiation.
José luis bustelo | Published Monday, September 01, 2025Negotiation plays a fundamental role in shaping human societies, underpinning conflict resolution, institutional design, and economic coordination. This article introduces E³-MAN, a novel multi-agent model for negotiation that integrates individual utility maximization with fairness and institutional legitimacy. Unlike classical approaches grounded solely in game theory, our model incorporates Bayesian opponent modeling, transfer learning from past negotiation domains, and fallback institutional rules to resolve deadlocks. Agents interact in dynamic environments characterized by strategic heterogeneity and asymmetric information, negotiating over multidimensional issues under time constraints. Through extensive simulation experiments, we compare E³-MAN against the Nash bargaining solution and equal-split baselines using key performance metrics: utilitarian efficiency, Nash social welfare, Jain fairness index, Gini coefficient, and institutional compliance. Results show that E³-MAN achieves near-optimal efficiency while significantly improving distributive equity and agreement stability. A legal application simulating multilateral labor arbitration demonstrates that institutional default rules foster more balanced outcomes and increase negotiation success rates from 58% to 98%. By combining computational intelligence with normative constraints, this work contributes to the growing field of socially aware autonomous agents. It offers a virtual laboratory for exploring how simple institutional interventions can enhance justice, cooperation, and robustness in complex socio-legal systems.
Introducing two extensions of Schelling's segregation model
Andreas Flache Carlos A. de Matos Fernandes | Published Monday, January 25, 2021Schelling famously proposed an extremely simple but highly illustrative social mechanism to understand how strong ethnic segregation could arise in a world where individuals do not necessarily want it. Schelling’s simple computational model is the starting point for our extensions in which we build upon Wilensky’s original NetLogo implementation of this model. Our two NetLogo models can be best studied while reading our chapter “Agent-based Computational Models” (Flache and de Matos Fernandes, 2021). In the chapter, we propose 10 best practices to elucidate how agent-based models are a unique method for providing and analyzing formally precise, and empirically plausible mechanistic explanations of puzzling social phenomena, such as segregation, in the social world. Our chapter addresses in particular analytical sociologists who are new to ABMs.
In the first model (SegregationExtended), we build on Wilensky’s implementation of Schelling’s model which is available in NetLogo library (Wilensky, 1997). We considerably extend this model, allowing in particular to include larger neighborhoods and a population with four groups roughly resembling the ethnic composition of a contemporary large U.S. city. Further features added concern the possibility to include random noise, and the addition of a number of new outcome measures tuned to highlight macro-level implications of the segregation dynamics for different groups in the agent society.
In SegregationDiscreteChoice, we further modify the model incorporating in particular three new features: 1) heterogeneous preferences roughly based on empirical research categorizing agents into low, medium, and highly tolerant within each of the ethnic subgroups of the population, 2) we drop global thresholds (%-similar-wanted) and introduce instead a continuous individual-level single-peaked preference function for agents’ ideal neighborhood composition, and 3) we use a discrete choice model according to which agents probabilistically decide whether to move to a vacant spot or stay in the current spot by comparing the attractiveness of both locations based on the individual preference functions.
…
Displaying 10 of 108 results for "P W Heijnen" clear search