The purpose of this model is to illustrate the use of agent-based computational modelling in the study of the emergence of reputation and status beliefs in a population.

The model simulates interactions in small, task focused groups that might lead to the emergence of status beliefs among group members.

This is a tool to explore the effects of groups´ spatial segregation on the emergence of opinion polarization. It embeds two opinion formation models: a model of negative (and positive) social influence and a model of persuasive argument exchange.

This model makes it possible to explore how network clustering and resistance to changing existing status beliefs might affect the spontaneous emergence and diffusion of such beliefs as described by status construction theory.

Schelling famously proposed an extremely simple but highly illustrative social mechanism to understand how strong ethnic segregation could arise in a world where individuals do not necessarily want it. Schelling’s simple computational model is the starting point for our extensions in which we build upon Wilensky’s original NetLogo implementation of this model. Our two NetLogo models can be best studied while reading our chapter “Agent-based Computational Models” (Flache and de Matos Fernandes, 2021). In the chapter, we propose 10 best practices to elucidate how agent-based models are a unique method for providing and analyzing formally precise, and empirically plausible mechanistic explanations of puzzling social phenomena, such as segregation, in the social world. Our chapter addresses in particular analytical sociologists who are new to ABMs.

In the first model (SegregationExtended), we build on Wilensky’s implementation of Schelling’s model which is available in NetLogo library (Wilensky, 1997). We considerably extend this model, allowing in particular to include larger neighborhoods and a population with four groups roughly resembling the ethnic composition of a contemporary large U.S. city. Further features added concern the possibility to include random noise, and the addition of a number of new outcome measures tuned to highlight macro-level implications of the segregation dynamics for different groups in the agent society.

In SegregationDiscreteChoice, we further modify the model incorporating in particular three new features: 1) heterogeneous preferences roughly based on empirical research categorizing agents into low, medium, and highly tolerant within each of the ethnic subgroups of the population, 2) we drop global thresholds (%-similar-wanted) and introduce instead a continuous individual-level single-peaked preference function for agents’ ideal neighborhood composition, and 3) we use a discrete choice model according to which agents probabilistically decide whether to move to a vacant spot or stay in the current spot by comparing the attractiveness of both locations based on the individual preference functions.

…

We extend the Flache-Mäs model to incorporate the location and dyadic communication regime of the agents in the opinion formation process. We make spatially proximate agents more likely to interact with each other in a pairwise communication regime.

Schelling and Sakoda prominently proposed computational models suggesting that strong ethnic residential segregation can be the unintended outcome of a self-reinforcing dynamic driven by choices of individuals with rather tolerant ethnic preferences. There are only few attempts to apply this view to school choice, another important arena in which ethnic segregation occurs. In the current paper, we explore with an agent-based theoretical model similar to those proposed for residential segregation, how ethnic tolerance among parents can affect the level of school segregation. More specifically, we ask whether and under which conditions school segregation could be reduced if more parents hold tolerant ethnic preferences. We move beyond earlier models of school segregation in three ways. First, we model individual school choices using a random utility discrete choice approach. Second, we vary the pattern of ethnic segregation in the residential context of school choices systematically, comparing residential maps in which segregation is unrelated to parents’ level of tolerance to residential maps reflecting their ethnic preferences. Third, we introduce heterogeneity in tolerance levels among parents belonging to the same group. Our simulation experiments suggest that ethnic school segregation can be a very robust phenomenon, occurring even when about half of the population prefers mixed to segregated schools. However, we also identify a “sweet spot” in the parameter space in which a larger proportion of tolerant parents makes the biggest difference. This is the case when parents have moderate preferences for nearby schools and there is only little residential segregation. Further experiments are presented that unravel the underlying mechanisms.

The model presented here is extensively described in the paper ‘Talk less to strangers: How homophily can improve collective decision-making in diverse teams’ (forthcoming at JASSS). A full replication package reproducing all results presented in the paper is accessible at https://osf.io/76hfm/.

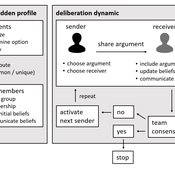
Narrative documentation includes a detailed description of the model, including a schematic figure and an extensive representation of the model in pseudocode.

The model develops a formal representation of a diverse work team facing a decision problem as implemented in the experimental setup of the hidden-profile paradigm. We implement a setup where a group seeks to identify the best out of a set of possible decision options. Individuals are equipped with different pieces of information that need to be combined to identify the best option. To this end, we assume a team of N agents. Each agent belongs to one of M groups where each group consists of agents who share a common identity.
The virtual teams in our model face a decision problem, in that the best option out of a set of J discrete options needs to be identified. Every team member forms her own belief about which decision option is best but is open to influence by other team members. Influence is implemented as a sequence of communication events. Agents choose an interaction partner according to homophily h and take turns in sharing an argument with an interaction partner. Every time an argument is emitted, the recipient updates her beliefs and tells her team what option she currently believes to be best. This influence process continues until all agents prefer the same option. This option is the team’s decision.

Agent-based model of hunting behavior of Ache hunter-gatherers from Paraguay. We evaluate the effect of group size and cooperative hunting

I model a forest and a community of loggers. Agents follow different kinds of rules in order to log. I compare the impact of endogenous and of exogenous institutions on the state of the forest and on the profit of the users, representing different scenarios of participatory conservation projects.