About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 31 results team clear search
E³-MAN. An Institutionally-guided multi-agent. Model for fair and efficient negotiation.
José luis bustelo | Published Monday, September 01, 2025Negotiation plays a fundamental role in shaping human societies, underpinning conflict resolution, institutional design, and economic coordination. This article introduces E³-MAN, a novel multi-agent model for negotiation that integrates individual utility maximization with fairness and institutional legitimacy. Unlike classical approaches grounded solely in game theory, our model incorporates Bayesian opponent modeling, transfer learning from past negotiation domains, and fallback institutional rules to resolve deadlocks. Agents interact in dynamic environments characterized by strategic heterogeneity and asymmetric information, negotiating over multidimensional issues under time constraints. Through extensive simulation experiments, we compare E³-MAN against the Nash bargaining solution and equal-split baselines using key performance metrics: utilitarian efficiency, Nash social welfare, Jain fairness index, Gini coefficient, and institutional compliance. Results show that E³-MAN achieves near-optimal efficiency while significantly improving distributive equity and agreement stability. A legal application simulating multilateral labor arbitration demonstrates that institutional default rules foster more balanced outcomes and increase negotiation success rates from 58% to 98%. By combining computational intelligence with normative constraints, this work contributes to the growing field of socially aware autonomous agents. It offers a virtual laboratory for exploring how simple institutional interventions can enhance justice, cooperation, and robustness in complex socio-legal systems.
Agent-Based Model for Multiple Team Membership (ABMMTM)
Andrew Collins | Published Thursday, April 03, 2025The Agent-Based Model for Multiple Team Membership (ABMMTM) simulates design teams searching for viable design solutions, for a large design project that requires multiple design teams that are working simultaneously, under different organizational structures; specifically, the impact of multiple team membership (MTM). The key mechanism under study is how individual agent-level decision-making impacts macro-level project performance, specifically, wage cost. Each agent follows a stochastic learning approach, akin to simulated annealing or reinforcement learning, where they iteratively explore potential design solutions. The agent evaluates new solutions based on a random-walk exploration, accepting improvements while rejecting inferior designs. This iterative process simulates real-world problem-solving dynamics where designers refine solutions based on feedback.
As a proof-of-concept demonstration of assessing the macro-level effects of MTM in organizational design, we developed this agent-based simulation model which was used in a simulation experiment. The scenario is a system design project involving multiple interdependent teams of engineering designers. In this scenario, the required system design is split into three separate but interdependent systems, e.g., the design of a satellite could (trivially) be split into three components: power source, control system, and communication systems; each of three design team is in charge of a design of one of these components. A design team is responsible for ensuring its proposed component’s design meets the design requirement; they are not responsible for the design requirements of the other components. If the design of a given component does not affect the design requirements of the other components, we call this the uncoupled scenario; otherwise, it is a coupled scenario.
Autonomy or control? An agent-based study of self-organising versus centralised task allocation
Shaoni Wang | Published Wednesday, January 29, 2025The aim of our model is to investigate the team dynamics through two types of task allocation strategies, with a focus on the dynamic interplay between individual needs and group performance. To achieve this goal, we have formulated an agent-based model (ABM) to formalize Deci & Ryan’s self-determination theory (SDT) and explore the social dynamics that govern the relationship between individual and group levels of team performance.
Team Structure and Task Performance
Davide Secchi Martin Neumann | Published Monday, August 05, 2024This model was designed to study resilience in organizations. Inspired by ethnographic work, it follows the simple goal to understand whether team structure affects the way in which tasks are performed. In so doing, it compares the ‘hybrid’ data-inspired structure with three more traditional structures (i.e. hierarchy, flexible/relaxed hierarchy, and anarchy/disorganization).
The influence of cognitive diversity on networked search and coordination
César García-Díaz | Published Wednesday, April 03, 2024Agent-based models of organizational search have long investigated how exploitative and exploratory behaviors shape and affect performance on complex landscapes. To explore this further, we build a series of models where agents have different levels of expertise and cognitive capabilities, so they must rely on each other’s knowledge to navigate the landscape. Model A investigates performance results for efficient and inefficient networks. Building on Model B, it adds individual-level cognitive diversity and interaction based on knowledge similarity. Model C then explores the performance implications of coordination spaces. Results show that totally connected networks outperform both hierarchical and clustered network structures when there are clear signals to detect neighbor performance. However, this pattern is reversed when agents must rely on experiential search and follow a path-dependent exploration pattern.
Role of Diversity in Team Performance: the Case of Missing Expertise, an Agent Based Simulations
Tamás Kiss | Published Friday, December 29, 2023This ABM simulates problem solving agents as they work on a set of tasks. Each agent has a trait vector describing their skills. Two agents might form a collaboration if their traits are similar enough. Tasks are defined by a component vector. Agents work on tasks by decreasing tasks’ component vectors towards zero.
The simulation generates agents with given intrapersonal functional diversity (IFD), and dominant function diversity (DFD), and a set of random tasks and evaluates how agents’ traits influence their level of communication and the performance of a team of agents.
Modeling results highlight the importance of the distributions of agents’ properties forming a team, and suggests that for a thorough description of management teams, not only diversity measures based on individual agents, but an aggregate measure is also required.
…
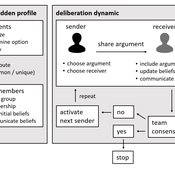
Agent-based model of team decision-making in hidden profile situations
Andreas Flache Jonas Stein Vincenz Frey | Published Thursday, April 20, 2023 | Last modified Friday, November 17, 2023The model presented here is extensively described in the paper ‘Talk less to strangers: How homophily can improve collective decision-making in diverse teams’ (forthcoming at JASSS). A full replication package reproducing all results presented in the paper is accessible at https://osf.io/76hfm/.
Narrative documentation includes a detailed description of the model, including a schematic figure and an extensive representation of the model in pseudocode.
The model develops a formal representation of a diverse work team facing a decision problem as implemented in the experimental setup of the hidden-profile paradigm. We implement a setup where a group seeks to identify the best out of a set of possible decision options. Individuals are equipped with different pieces of information that need to be combined to identify the best option. To this end, we assume a team of N agents. Each agent belongs to one of M groups where each group consists of agents who share a common identity.
The virtual teams in our model face a decision problem, in that the best option out of a set of J discrete options needs to be identified. Every team member forms her own belief about which decision option is best but is open to influence by other team members. Influence is implemented as a sequence of communication events. Agents choose an interaction partner according to homophily h and take turns in sharing an argument with an interaction partner. Every time an argument is emitted, the recipient updates her beliefs and tells her team what option she currently believes to be best. This influence process continues until all agents prefer the same option. This option is the team’s decision.
The S-uFUNK Model
Davide Secchi | Published Friday, March 17, 2023This version 2.1.0 of the uFunk model is about setting a business strategy (the S in the name) for an organization. A team of managers (or executives) meet and discuss various options on the strategy for the firm. There are three aspects that they have to agree on to set the strategic positioning of the organization.
The discussion is on market, stakeholders, and resources. The team (it could be a business strategy task force) considers various aspects of these three elements. The resources they use to develop the discussion can come from a traditional approach to strategy or from non-traditional means (e.g., so-called serious play, creativity and imagination techniques).
The S-uFunk 2.1.0 Model wants to understand to which extent cognitive means triggered by traditional and non-traditional resources affect the making of the strategy process.
NK model for multilevel adaptation
Dario Blanco Fernandez | Published Wednesday, November 30, 2022Previous research on organizations often focuses on either the individual, team, or organizational level. There is a lack of multidimensional research on emergent phenomena and interactions between the mechanisms at different levels. This paper takes a multifaceted perspective on individual learning and autonomous group formation and turnover. To analyze interactions between the two levels, we introduce an agent-based model that captures an organization with a population of heterogeneous agents who learn and are limited in their rationality. To solve a task, agents form a group that can be adapted from time to time. We explore organizations that promote learning and group turnover either simultaneously or sequentially and analyze the interactions between the activities and the effects on performance. We observe underproportional interactions when tasks are interdependent and show that pushing learning and group turnover too far might backfire and decrease performance significantly.
Peer reviewed A Computational Simulation for Task Allocation Influencing Performance in the Team System
Shaoni Wang | Published Friday, November 11, 2022 | Last modified Thursday, April 06, 2023This model system aims to simulate the whole process of task allocation, task execution and evaluation in the team system through a feasible method. On the basis of Complex Adaptive Systems (CAS) theory and Agent-based Modelling (ABM) technologies and tools, this simulation system attempts to abstract real-world teams into MAS models. The author designs various task allocation strategies according to different perspectives, and the interaction among members is concerned during the task-performing process. Additionally, knowledge can be acquired by such an interaction process if members encounter tasks they cannot handle directly. An artificial computational team is constructed through ABM in this simulation system, to replace real teams and carry out computational experiments. In all, this model system has great potential for studying team dynamics, and model explorers are encouraged to expand on this to develop richer models for research.
Displaying 10 of 31 results team clear search