About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 186 results for "Kasper H Kisjes" clear search
The Friendship Field
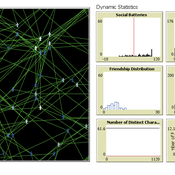
Eva Timmer Chrisja van de Kieft | Published Thursday, May 26, 2022 | Last modified Tuesday, August 30, 2022The Friendship Field model aims at modelling friendship formation based on three factors: Extraversion, Resemblance and Status, where social interaction is motivated by the Social Battery. Social Battery is one’s energy and motivation to engage in social contact. Since social contact is crucial for friendship formation, the model included Social Battery to affect social interactions. To our best knowledge, Social Battery is a yet unintroduced concept in research while it is a dynamic factor influencing the social interaction besides one’s characteristics. Extraverts’ Social Batteries charge while interacting and exhaust while being alone. Introverts’ Social Batteries charge while being alone and exhaust while interacting. The aim of the model is to illustrate the concept of Social Battery. Moreover, the Friendship Field shows patterns regarding Extraversion, Resemblance and Status including the mere-exposure effect and friendship by similarity. For the implementation of Status, Kemper’s status-power theory is used. The concept of Social Battery is also linked to Kemper’s theory on the organism as reference group. By running the model for a year (3 interactions moments per day), the friendship dynamics over time can be studied.
We presented the model at the Social Simulation Conference 2022.
Peer reviewed The Archaeological Sampling Experimental Laboratory (tASEL)
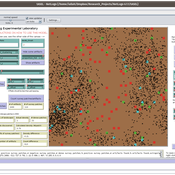
Isaac Ullah | Published Friday, March 11, 2022 | Last modified Wednesday, June 01, 2022The Archaeological Sampling Experimental Laboratory (tASEL) is an interactive tool for setting up and conducting experiments about sampling strategies for archaeological excavation, survey, and prospection.
ABM for Underwater optical wireless communication in a water tank
Mohamed ABID | Published Sunday, May 29, 2022This model simulates the propagation of photons in a water tank. A source of light emits an impulse of photons with equal energy represented by yellow dots. These photons are then scattered by water particles before possibly reaching the photo-detector represented by a gray line. Different types of water are considered. For each one of them we calculate the total received energy.
The water tank is represented by a blue rectangle with fixed dimensions. It’s exposed to the air interface and has totally absorbent barriers. Four types of water are supported. Each one is characterized by its absorption and scattering coefficients.
At the source, the photons are generated uniformly with a random direction within the beamwidth. Each photon travels a random distance drawn from a distribution depending on the water characteristics before encountering a water particle.
Based on the updated position of the photon, three situations may occur:
-The photon hits the barrier of the tank on its trajectory. In this case it’s considered as lost since the barriers are assumed totally absorbent.
…
Development of coral reefs under climate change impacts and adaptation options
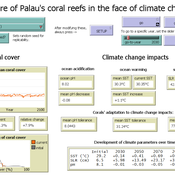
Nina Preußler | Published Friday, May 30, 2025This NetLogo model simulates how coral reefs around the islands of Palau would develop under different emission scenarios and with selected adaptation strategies. Reef health is indicated by coral cover (%) and is affected by four major climate change impacts: increasing sea surface temperature, sea level rise, ocean acidification, and more intense typhoons. The model differentiates between inner and outer reefs, with the former naturally adapted to warmer, more acidic waters. The simulation includes bleaching events and possible recovery. In addition, the user can choose between different coral transplantation strategies as well as regulate natural thermal adaptation rates.
Schelling Model of the City of Salzburg
Andreas Schlagbauer | Published Monday, December 05, 2022The purpose of the model is to better understand, how different factors for human residential choices affect the city’s segregation pattern. Therefore, a Schelling (1971) model was extended to include ethnicity, income, and affordability and applied to the city of Salzburg. So far, only a few studies have tried to explore the effect of multiple factors on the residential pattern (Sahasranaman & Jensen, 2016, 2018; Yin, 2009). Thereby, models using multiple factors can produce more realistic results (Benenson et al., 2002). This model and the corresponding thesis aim to fill that gap.
Peer reviewed A Bayesian Nash Equilibrium (BNE)-informed ABM for pedestrian evacuation in different constricted spaces
Jiaqi Ge Yiyu Wang Alexis Comber | Published Wednesday, October 11, 2023This BNE-informed ABM ultimately aims to provide a more realistic description of complicated pedestrian behaviours especially in high-density and life-threatening situations. Bayesian Nash Equilibrium (BNE) was adopted to reproduce interactive decision-making process among rational and game-playing agents. The implementations of 3 behavioural models, which are Shortest Route (SR) model, Random Follow (RF) model, and BNE model, make it possible to simulate emergent patterns of pedestrian behaviours (e.g. herding and self-organised queuing behaviours, etc.) in emergency situations.
According to the common features of previous mass trampling accidents, a series of simulation experiments were performed in space with 3 types of barriers, which are Horizontal Corridors, Vertical Corridors, and Random Squares, standing for corridors, bottlenecks and intersections respectively, to investigate emergent behaviours of evacuees in varied constricted spatial environments. The output of this ABM has been available at https://data.mendeley.com/datasets/9v4byyvgxh/1.
Peer reviewed AgModel
Isaac Ullah | Published Friday, December 06, 2024AgModel is an agent-based model of the forager-farmer transition. The model consists of a single software agent that, conceptually, can be thought of as a single hunter-gather community (i.e., a co-residential group that shares in subsistence activities and decision making). The agent has several characteristics, including a population of human foragers, intrinsic birth and death rates, an annual total energy need, and an available amount of foraging labor. The model assumes a central-place foraging strategy in a fixed territory for a two-resource economy: cereal grains and prey animals. The territory has a fixed number of patches, and a starting number of prey. While the model is not spatially explicit, it does assume some spatiality of resources by including search times.
Demographic and environmental components of the simulation occur and are updated at an annual temporal resolution, but foraging decisions are “event” based so that many such decisions will be made in each year. Thus, each new year, the foraging agent must undertake a series of optimal foraging decisions based on its current knowledge of the availability of cereals and prey animals. Other resources are not accounted for in the model directly, but can be assumed for by adjusting the total number of required annual energy intake that the foraging agent uses to calculate its cereal and prey animal foraging decisions. The agent proceeds to balance the net benefits of the chance of finding, processing, and consuming a prey animal, versus that of finding a cereal patch, and processing and consuming that cereal. These decisions continue until the annual kcal target is reached (balanced on the current human population). If the agent consumes all available resources in a given year, it may “starve”. Starvation will affect birth and death rates, as will foraging success, and so the population will increase or decrease according to a probabilistic function (perturbed by some stochasticity) and the agent’s foraging success or failure. The agent is also constrained by labor caps, set by the modeler at model initialization. If the agent expends its yearly budget of person-hours for hunting or foraging, then the agent can no longer do those activities that year, and it may starve.
Foragers choose to either expend their annual labor budget either hunting prey animals or harvesting cereal patches. If the agent chooses to harvest prey animals, they will expend energy searching for and processing prey animals. prey animals search times are density dependent, and the number of prey animals per encounter and handling times can be altered in the model parameterization (e.g. to increase the payoff per encounter). Prey animal populations are also subject to intrinsic birth and death rates with the addition of additional deaths caused by human predation. A small amount of prey animals may “migrate” into the territory each year. This prevents prey animals populations from complete decimation, but also may be used to model increased distances of logistic mobility (or, perhaps, even residential mobility within a larger territory).
…
Team Structure and Task Performance
Davide Secchi Martin Neumann | Published Monday, August 05, 2024This model was designed to study resilience in organizations. Inspired by ethnographic work, it follows the simple goal to understand whether team structure affects the way in which tasks are performed. In so doing, it compares the ‘hybrid’ data-inspired structure with three more traditional structures (i.e. hierarchy, flexible/relaxed hierarchy, and anarchy/disorganization).
E³-MAN. An Institutionally-guided multi-agent. Model for fair and efficient negotiation.
José luis bustelo | Published Monday, September 01, 2025Negotiation plays a fundamental role in shaping human societies, underpinning conflict resolution, institutional design, and economic coordination. This article introduces E³-MAN, a novel multi-agent model for negotiation that integrates individual utility maximization with fairness and institutional legitimacy. Unlike classical approaches grounded solely in game theory, our model incorporates Bayesian opponent modeling, transfer learning from past negotiation domains, and fallback institutional rules to resolve deadlocks. Agents interact in dynamic environments characterized by strategic heterogeneity and asymmetric information, negotiating over multidimensional issues under time constraints. Through extensive simulation experiments, we compare E³-MAN against the Nash bargaining solution and equal-split baselines using key performance metrics: utilitarian efficiency, Nash social welfare, Jain fairness index, Gini coefficient, and institutional compliance. Results show that E³-MAN achieves near-optimal efficiency while significantly improving distributive equity and agreement stability. A legal application simulating multilateral labor arbitration demonstrates that institutional default rules foster more balanced outcomes and increase negotiation success rates from 58% to 98%. By combining computational intelligence with normative constraints, this work contributes to the growing field of socially aware autonomous agents. It offers a virtual laboratory for exploring how simple institutional interventions can enhance justice, cooperation, and robustness in complex socio-legal systems.
This model extends the original Artifical Anasazi (AA) model to include individual agents, who vary in age and sex, and are aggregated into households. This allows more realistic simulations of population dynamics within the Long House Valley of Arizona from AD 800 to 1350 than are possible in the original model. The parts of this model that are directly derived from the AA model are based on Janssen’s 1999 Netlogo implementation of the model; the code for all extensions and adaptations in the model described here (the Artificial Long House Valley (ALHV) model) have been written by the authors. The AA model included only ideal and homogeneous “individuals” who do not participate in the population processes (e.g., birth and death)–these processes were assumed to act on entire households only. The ALHV model incorporates actual individual agents and all demographic processes affect these individuals. Individuals are aggregated into households that participate in annual agricultural and demographic cycles. Thus, the ALHV model is a combination of individual processes (birth and death) and household-level processes (e.g., finding suitable agriculture plots).
As is the case for the AA model, the ALHV model makes use of detailed archaeological and paleoenvironmental data from the Long House Valley and the adjacent areas in Arizona. It also uses the same methods as the original model (from Janssen’s Netlogo implementation) to estimate annual maize productivity of various agricultural zones within the valley. These estimates are used to determine suitable locations for households and farms during each year of the simulation.
Displaying 10 of 186 results for "Kasper H Kisjes" clear search