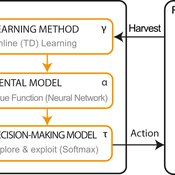
The model is a stylized representation of a social-ecological system of agents moving and harvesting a renewable resource. The purpose is to analyze how mobility affects sustainability. Experiments changing agents’ mobility, landscape and information governments have can be run.

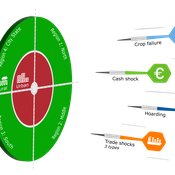
Food trade networks represent a complex system where food is periodically produced in different regions of the world. Food is continuously stocked and traded. Food security in a globalised world is vulnerable to shocks. We present DARTS, a new agent based model that models monthly dynamics of food production, trade, stocking, consumption and food security for different interconnected world regions and a city state. Agents in different regions differ in their harvest seasons, wealth (rich and poor), degree of urbanisation and connection to domestic and global markets. DARTS was specifically designed to model direct and indirect effects of shocks in the food system. We introduce a new typology of 6 distinct shock types and analyse their impact on food security, modelling local and global effects and short term and longer term effects. An second important scientific novelty of the model is that DARTS can also model indirect effects of shocks (cascading in space and in time, lag effects due to trade and food stock buffering). A third important scientific novelty of the model is its’ capability of modelling food security at different scales, in which the rural/urban divide and differences in (intra-annually varying) production and trade connections play a key role. At the time of writing DARTS is yet insufficiently parameterised for accurate prediction for real world regions and cities. Simulations for a hypothetical in silico world with 3 regions and a city state show that DARTS can reproduce rich and complex dynamics with analogues in the real world. The scientific interest is more on deepening insight in process dynamics and chains of events that lead to ultimate shock effects on food security.

This is a model of the occurrence of disorganization and its impact on individual goal setting and problem-solving. This model therefore, explores the effects of disorganization on goal achievement.

This research aims to uncover the micro-mechanisms that drive the macro-level relationship between cultural tolerance and innovation. We focus on the indirect influence of minorities—specifically, workers with diverse domain expertise—within collaboration networks. We propose that minority influence from individuals with different expertise can serve as a key driver of organizational innovation, particularly in dynamic market environments, and that cultural tolerance is critical for enabling such minority-induced innovation. Our model demonstrates that seemingly conflicting empirical patterns between cultural tightness/looseness and innovation can emerge from the same underlying micro-mechanisms, depending on parameter values. A systematic simulation experiment revealed an optimal cultural configuration: a medium level of tolerance (t = 0.6) combined with low consistency (κ = 0.05) produced the fastest adaptation to abrupt market changes. These findings provide evidence that indirect minority influence is a core micro-mechanism linking cultural tolerance to innovation.

Purpose of the model is to perform a “virtual experiment” to test the predator satiation hypothesis, advanced in literature to explain the mast seeding phenomenon.

MoPAgrIB model simulates the movement of cultivated patches in a savannah vegetation mosaic ; how they move and relocate through the landscape, depending on farming practices, population growth, social rules and vegetation growth.

This is a simulation model of an intelligent agent that has the objective to learn sustainable management of a renewable resource, such as a fish stock.

We study the impact of endogenous creation and destruction of social ties in an artificial society on aggregate outcomes such as generalized trust, willingness to cooperate, social utility and economic performance. To this end we put forward a computational multi-agent model where agents of overlapping generations interact in a dynamically evolving social network. In the model, four distinct dimensions of individuals’ social capital: degree, centrality, heterophilous and homophilous interactions, determine their generalized trust and willingness to cooperate, altogether helping them achieve certain levels of social utility (i.e., utility from social contacts) and economic performance. We find that the stationary state of the simulated social network exhibits realistic small-world topology. We also observe that societies whose social networks are relatively frequently reconfigured, display relatively higher generalized trust, willingness to cooperate, and economic performance – at the cost of lower social utility. Similar outcomes are found for societies where social tie dissolution is relatively weakly linked to family closeness.

The Holmestrand model is an epidemiological agent-based model. Its aim is to test hypotheses related to how the social and physical environment of a residential school for children with disabilities might influence the spread of an infectious disease epidemic among students and staff. Annual reports for the Holmestrand School for the Deaf (Norway) are the primary sources of inspiration for the modeled school, with additional insights drawn from other archival records for schools for children with disabilities in early 20th century Norway and data sources for the 1918 influenza pandemic. The model environment consists of a simplified boarding school that includes residential spaces for students and staff, classrooms, a dining room, common room, and an outdoor area. Students and staff engage in activities reflecting hourly schedules suggested by school reports. By default, a random staff member is selected as the first case and is infected with disease. Subsequent transmission is determined by agent movement and interactions between susceptible and infectious pairs.

The model is suitable to investigate the effects of different characteristics of apprenticeship programmes both in historical and contemporary societies. The model is built considering five societies, using an agent-based simulation model, we identified six main characteristics which impact the success of an apprenticeship programme in a society, which we measured by considering three parameters, namely the number of skilled agents produced by the apprenticeships, programme completion, and the contribution of programmes in the Gross Domestic Income (GDI) of the society. We investigate different definitions for success of an apprenticeship and some hypothetical societies to test some common beliefs about apprenticeships performance. The model also shows the number of unemployed agents given their work-based skills, wages, and the number of small and large companies who participate in training agents. The model enables exploring the impact of parameters, such as initial wages and the number of training years, along with the stated policies on the system.