About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 140 results for "Sandra H Goff" clear search
PopComp
Andre Costopoulos | Published Thursday, December 10, 2020PopComp by Andre Costopoulos 2020
[email protected]
Licence: DWYWWI (Do whatever you want with it)
I use Netlogo to build a simple environmental change and population expansion and diffusion model. Patches have a carrying capacity and can host two kinds of populations (APop and BPop). Each time step, the carrying capacity of each patch has a given probability of increasing or decreasing up to a maximum proportion.
…
Peer reviewed AgentEx
Nanda Wijermans Maja Schlüter Caroline Schill Therese Lindahl | Published Sunday, November 13, 2016AgentEx aims to advance understanding of group processes for sustainable management of a common pool resource (CPR). By supporting the development and test explanations of cooperation and sustainable exploitation.
Online Protest and Repression in Authoritarian Settings (OPRAS)
Nanda Wijermans Annie Waldherr Aytalina Kulichkina | Published Tuesday, January 27, 2026This agent-based model, developed for the study “Online Protest and Repression in Authoritarian Settings,” examines how online protest and repression evolve in authoritarian contexts and how these dynamics affect ordinary users’ attitudes and behavior on social media. The model integrates key theoretical and empirical insights into social media use and core political factors that shape digital contention in authoritarian settings. The following questions are addressed: (1) how online protest–repression dynamics unfold across different levels of authoritarianism and varying compositions of committed accounts, and (2) how ordinary users’ internal propensity to protest and their perceived probability of successful repression change during online protest-repression contestation. The model is evaluated against two empirically grounded macro patterns observed in the real world. The first is enduring protest: online protest becomes dominant as vocal protesters grow to outnumber vocal repressors, shrinking the pool of silent users and stabilizing a pro-protest majority. The second is suppressed protest: online dissent is contained as vocal repression and silence expand in response to protest, yielding a sustained majority of repressive and silent accounts. Together, these dynamics demonstrate how dissenting voices are empowered and suppressed online in authoritarian settings.
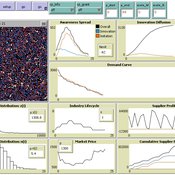
(Policy induced) Diffusion of Innovations - An integrated demand-supply Model based on Cournot Competition
Martin Rixin | Published Monday, August 29, 2011 | Last modified Saturday, April 27, 2013Objective is to simulate policy interventions in an integrated demand-supply model. The underlying demand function links both sides. Diffusion proceeds if interactions distribute awareness (Epidemic effect) and rivalry reduces the market price (Probit effect). Endogeneity is given due to the fact that consumer awareness as well as their willingness-to-pay drives supply-side rivalry. Firm´s entry and exit decisions as well as quantity and price settings are driven by Cournot competition.
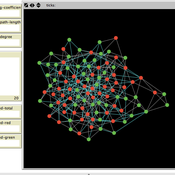
Homophily-driven Network Evolution and Diffusion
Gönenç Yücel Mustafa Yavaş | Published Thursday, January 08, 2015The model is an experimental ground to study the impact of network structure on diffusion. It allows to construct a social network that already has some measurable level of homophily, and simulate a diffusion process over this social network.
04 TpLab V2.08 – Teleological Pruning Laboratory
Garvin Boyle | Published Saturday, April 15, 2017Our societal belief systems are pruned by evolution, informing our unsustainable economies. This is one of a series of models exploring the dynamics of sustainable economics – PSoup, ModEco, EiLab, OamLab, MppLab, TpLab, CmLab.
Policy Formulation for Public Administration - Innovation
Bashar Ourabi | Published Tuesday, August 29, 2017 | Last modified Tuesday, August 29, 2017Innovation a byproduct of the intellectual capital, requires a new paradigm for the production constituents. Human Capital HC,Structural capital SC and relational capital RC become key for intellectual capital and consequently for innovation.
A discrete-time stochastic model with state-dependent transmission probabilities and multi-agent simulations focusing on possible risks that could materialize in the final phase of the epidemic.
A Mathematical Model of The Beer Game
Hakan Yasarcan Mert Edali | Published Wednesday, November 05, 2014This is the R code of the mathematical model that includes the decision making formulations for artificial agents. This code corresponds to equations 1-70 given in the paper “A Mathematical Model of The Beer Game”.
A Mathematical Model of The Beer Game Coded in R for Verification
Hakan Yasarcan Mert Edali | Published Wednesday, November 05, 2014This is the R code of the mathematical model used for verification. This code corresponds to equations 1-9, 15-53, 58-62, 69-70, and 72-75 given in the paper “A Mathematical Model of The Beer Game”.
Displaying 10 of 140 results for "Sandra H Goff" clear search