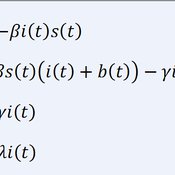About the CoMSES Model Library more info
Our mission is to help computational modelers at all levels engage in the establishment and adoption of community standards and good practices for developing and sharing computational models. Model authors can freely publish their model source code in the Computational Model Library alongside narrative documentation, open science metadata, and other emerging open science norms that facilitate software citation, reproducibility, interoperability, and reuse. Model authors can also request peer review of their computational models to receive a DOI.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with additional detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 3 of 3 results product diffusion clear search
Product Diffusion Model in an Advance Selling Strategy
Peng Shao | Published Tuesday, March 15, 2016 | Last modified Tuesday, March 15, 2016the model can be used to describe the product diffusion in an Advance Selling Strategy. this model takes into account the consumers product adoption, and describe consumer’s online behavior based on four states.
(Policy induced) Diffusion of Innovations - An integrated demand-supply Model based on Cournot Competition
Martin Rixin | Published Monday, August 29, 2011 | Last modified Saturday, April 27, 2013Objective is to simulate policy interventions in an integrated demand-supply model. The underlying demand function links both sides. Diffusion proceeds if interactions distribute awareness (Epidemic effect) and rivalry reduces the market price (Probit effect). Endogeneity is given due to the fact that consumer awareness as well as their willingness-to-pay drives supply-side rivalry. Firm´s entry and exit decisions as well as quantity and price settings are driven by Cournot competition.
An agent based simulation and data mining framework for scenario analysis of technology products
Moeed Haghnevis | Published Monday, December 13, 2010 | Last modified Saturday, April 27, 2013The objective of this study is to create a framework to simulate and analyze the effect of multiple business scenarios on the adoption behavior of a group of technology products.