About the CoMSES Model Library more info
Our mission is to help computational modelers at all levels engage in the establishment and adoption of community standards and good practices for developing and sharing computational models. Model authors can freely publish their model source code in the Computational Model Library alongside narrative documentation, open science metadata, and other emerging open science norms that facilitate software citation, reproducibility, interoperability, and reuse. Model authors can also request peer review of their computational models to receive a DOI.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with additional detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 110 results random clear search
Two agent-based models of cooperation in dynamic groups and fixed social networks
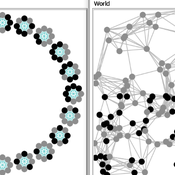
Carlos A. de Matos Fernandes | Published Thursday, January 20, 2022Both models simulate n-person prisoner dilemma in groups (left figure) where agents decide to C/D – using a stochastic threshold algorithm with reinforcement learning components. We model fixed (single group ABM) and dynamic groups (bad-barrels ABM). The purpose of the bad-barrels model is to assess the impact of information during meritocratic matching. In the bad-barrels model, we incorporated a multidimensional structure in which agents are also embedded in a social network (2-person PD). We modeled a random and homophilous network via a random spatial graph algorithm (right figure).
Space colonization
allagonne | Published Wednesday, January 05, 2022Agent-Based-Modeling - space colonization
ask me for the .nlogo model
WHAT IS IT?
The goal of this project is to simulate with NetLogo (v6.2) a space colonization of humans, starting from Earth, into the Milky Way.
HOW IT WORKS
…
Information Spread
Aaron Beck | Published Thursday, December 02, 2021Our model shows how disinformation spreads on a random network of individuals. The network is weighted and directed. We are looking at how different factors affect how fast, or how many people get “infected” with the misinformation. One of the main factors that we were curious about was perceived trustworthiness. This is because we want to see if people of power, or a high degree of perceived trustworthiness, were able to push misinformation to more people and convert more people to believe the information.
Simulating changing traffic flow caused by new bus route in Augsburg
Eduard | Published Wednesday, August 04, 2021This is a Netlogo model which simulates car and bus/tram traffic in Augsburg, specifically between the districts Stadtbergen, Göggingen and the Königsplatz. People either use their cars or public transport to travel to one of their random destinations (Stadtbergen or Göggingen), performing some activity and then returning to their home. Attributes such as travel and waiting time as well as their happiness upon arriving are stored and have an impact on individuals on whether they would consider changing their mode of transport or not.
Holmestrand School Model
Jessica Dimka | Published Friday, June 18, 2021 | Last modified Friday, April 29, 2022The Holmestrand model is an epidemiological agent-based model. Its aim is to test hypotheses related to how the social and physical environment of a residential school for children with disabilities might influence the spread of an infectious disease epidemic among students and staff. Annual reports for the Holmestrand School for the Deaf (Norway) are the primary sources of inspiration for the modeled school, with additional insights drawn from other archival records for schools for children with disabilities in early 20th century Norway and data sources for the 1918 influenza pandemic. The model environment consists of a simplified boarding school that includes residential spaces for students and staff, classrooms, a dining room, common room, and an outdoor area. Students and staff engage in activities reflecting hourly schedules suggested by school reports. By default, a random staff member is selected as the first case and is infected with disease. Subsequent transmission is determined by agent movement and interactions between susceptible and infectious pairs.
Sensitivity of the Deffuant model to measurement error
Dino Carpentras | Published Monday, June 07, 2021This code can be used to analyze the sensitivity of the Deffuant model to different measurement errors. Specifically to:
- Intrinsic stochastic error
- Binning of the measurement scale
- Random measurement noise
- Psychometric distortions
…
Introducing two extensions of Schelling's segregation model
Andreas Flache Carlos A. de Matos Fernandes | Published Monday, January 25, 2021Schelling famously proposed an extremely simple but highly illustrative social mechanism to understand how strong ethnic segregation could arise in a world where individuals do not necessarily want it. Schelling’s simple computational model is the starting point for our extensions in which we build upon Wilensky’s original NetLogo implementation of this model. Our two NetLogo models can be best studied while reading our chapter “Agent-based Computational Models” (Flache and de Matos Fernandes, 2021). In the chapter, we propose 10 best practices to elucidate how agent-based models are a unique method for providing and analyzing formally precise, and empirically plausible mechanistic explanations of puzzling social phenomena, such as segregation, in the social world. Our chapter addresses in particular analytical sociologists who are new to ABMs.
In the first model (SegregationExtended), we build on Wilensky’s implementation of Schelling’s model which is available in NetLogo library (Wilensky, 1997). We considerably extend this model, allowing in particular to include larger neighborhoods and a population with four groups roughly resembling the ethnic composition of a contemporary large U.S. city. Further features added concern the possibility to include random noise, and the addition of a number of new outcome measures tuned to highlight macro-level implications of the segregation dynamics for different groups in the agent society.
In SegregationDiscreteChoice, we further modify the model incorporating in particular three new features: 1) heterogeneous preferences roughly based on empirical research categorizing agents into low, medium, and highly tolerant within each of the ethnic subgroups of the population, 2) we drop global thresholds (%-similar-wanted) and introduce instead a continuous individual-level single-peaked preference function for agents’ ideal neighborhood composition, and 3) we use a discrete choice model according to which agents probabilistically decide whether to move to a vacant spot or stay in the current spot by comparing the attractiveness of both locations based on the individual preference functions.
…
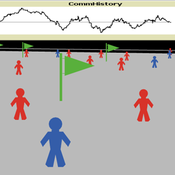
Model of communication between two groups of managers in the course of project implementation
Smarzhevskiy Ivan | Published Monday, December 07, 2020This is a simulation model of communication between two groups of managers in the course of project implementation. The “world” of the model is a space of interaction between project participants, each of which belongs either to a group of work performers or to a group of customers. Information about the progress of the project is publicly available and represents the deviation Earned value (EV) from the planned project value (cost baseline).
The key elements of the model are 1) persons belonging to a group of customers or performers, 2) agents that are communication acts. The life cycle of persons is equal to the time of the simulation experiment, the life cycle of the communication act is 3 periods of model time (for the convenience of visualizing behavior during the experiment). The communication act occurs at a specific point in the model space, the coordinates of which are realized as random variables. During the experiment, persons randomly move in the model space. The communication act involves persons belonging to a group of customers and a group of performers, remote from the place of the communication act at a distance not exceeding the value of the communication radius (MaxCommRadius), while at least one representative from each of the groups must participate in the communication act. If none are found, the communication act is not carried out. The number of potential communication acts per unit of model time is a parameter of the model (CommPerTick).
The managerial sense of the feedback is the stimulating effect of the positive value of the accumulated communication complexity (positive background of the project implementation) on the productivity of the performers. Provided there is favorable communication (“trust”, “mutual understanding”) between the customer and the contractor, it is more likely that project operations will be performed with less lag behind the plan or ahead of it.
The behavior of agents in the world of the model (change of coordinates, visualization of agents’ belonging to a specific communicative act at a given time, etc.) is not informative. Content data are obtained in the form of time series of accumulated communicative complexity, the deviation of the earned value from the planned value, average indicators characterizing communication - the total number of communicative acts and the average number of their participants, etc. These data are displayed on graphs during the simulation experiment.
The control elements of the model allow seven independent values to be varied, which, even with a minimum number of varied values (three: minimum, maximum, optimum), gives 3^7 = 2187 different variants of initial conditions. In this case, the statistical processing of the results requires repeated calculation of the model indicators for each grid node. Thus, the set of varied parameters and the range of their variation is determined by the logic of a particular study and represents a significant narrowing of the full set of initial conditions for which the model allows simulation experiments.
…
Change and Senescence
André Martins | Published Tuesday, November 10, 2020Agers and non-agers agent compete over a spatial landscape. When two agents occupy the same grid, who will survive is decided by a random draw where chances of survival are proportional to fitness. Agents have offspring each time step who are born at a distance b from the parent agent and the offpring inherits their genetic fitness plus a random term. Genetic fitness decreases with time, representing environmental change but effective non-inheritable fitness can increase as animals learn and get bigger.
Can ethnic tolerance curb self-reinforcing school segregation? A theoretical Agent Based Model
Lucas Sage Andreas Flache | Published Monday, August 10, 2020Schelling and Sakoda prominently proposed computational models suggesting that strong ethnic residential segregation can be the unintended outcome of a self-reinforcing dynamic driven by choices of individuals with rather tolerant ethnic preferences. There are only few attempts to apply this view to school choice, another important arena in which ethnic segregation occurs. In the current paper, we explore with an agent-based theoretical model similar to those proposed for residential segregation, how ethnic tolerance among parents can affect the level of school segregation. More specifically, we ask whether and under which conditions school segregation could be reduced if more parents hold tolerant ethnic preferences. We move beyond earlier models of school segregation in three ways. First, we model individual school choices using a random utility discrete choice approach. Second, we vary the pattern of ethnic segregation in the residential context of school choices systematically, comparing residential maps in which segregation is unrelated to parents’ level of tolerance to residential maps reflecting their ethnic preferences. Third, we introduce heterogeneity in tolerance levels among parents belonging to the same group. Our simulation experiments suggest that ethnic school segregation can be a very robust phenomenon, occurring even when about half of the population prefers mixed to segregated schools. However, we also identify a “sweet spot” in the parameter space in which a larger proportion of tolerant parents makes the biggest difference. This is the case when parents have moderate preferences for nearby schools and there is only little residential segregation. Further experiments are presented that unravel the underlying mechanisms.
Displaying 10 of 110 results random clear search