About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 487 results for "Tim M Daw" clear search
This is the R code of the mathematical model that includes the decision making formulations for artificial agents. Plus, the code for graphical output is also added to the original code.
Sunshine or Shield?: Secret Voting Procedures and Legislative Accountability
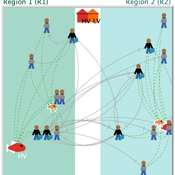
Matthew Taylor Michele Buttò Carlos Pereira | Published Tuesday, June 24, 2014 | Last modified Monday, April 08, 2019An agent-based model is used to simulate legislators’ behavior under secret voting rules, as influenced by the power of the accused politician, the composition of the voting body, and the publicity of the accusations.
Peer reviewed Small-Trade Model
Emilie Lindkvist Maja Schlüter Blanca Gonzalez-Mon Örjan Bodin | Published Wednesday, July 28, 2021The purpose of this model is to understand the role of trade networks and their interaction with different fish resources, for fish provision. The model is developed based on a multi-methods approach, combining agent-based modeling, network analysis and qualitative data based on a small-scale fisheries study case. The model can be used to investigate both how trade network structures are embedded in a social-ecological context and the trade processes that occur within them, to analyze how they lead to emergent outcomes related to the resilience of fish provision. The model processes are informed by qualitative data analysis, and the social network analysis of an empirical fish trade network. The network analysis can be used to investigate diverse network structures to perform model experiments, and their influence on model outcomes.
The main outcomes we study are 1) the overexploitation of fish resources and 2) the availability and variability of fish provision to satisfy different market demands, and 3) individual traders’ fish supply at the micro-level. The model has two types of trader agents, seller and dealer. The model reveals that the characteristics of the trade networks, linked to different trader types (that have different roles in those networks), can affect the resilience of fish provision.
Peer reviewed Egalitarian sharing
Marcos Pinheiro | Published Friday, January 27, 2023The model explores food distribution patterns that emerge in a small-scale non-agricultural group when individuals follow a set of spatially explicit sharing interaction rules derived from a theory on the evolution of the egalitarian social instinct.
SBH trust model
Di Wang | Published Tuesday, December 14, 2010 | Last modified Saturday, April 27, 2013This is a computational model to articulate the theory and test some assumption and axioms for the trust model and its relationship to SBH.
RiskNetABM
Birgit Müller Jürgen Groeneveld Karin Frank Meike Will Friederike Lenel | Published Monday, July 20, 2020 | Last modified Monday, May 03, 2021The fight against poverty is an urgent global challenge. Microinsurance is promoted as a valuable instrument for buffering income losses due to health or climate-related risks of low-income households in developing countries. However, apart from direct positive effects they can have unintended side effects when insured households lower their contribution to traditional arrangements where risk is shared through private monetary support.
RiskNetABM is an agent-based model that captures dynamics between income losses, insurance payments and informal risk-sharing. The model explicitly includes decisions about informal transfers. It can be used to assess the impact of insurance products and informal risk-sharing arrangements on the resilience of smallholders. Specifically, it allows to analyze whether and how economic needs (i.e. level of living costs) and characteristics of extreme events (i.e. frequency, intensity and type of shock) influence the ability of insurance and informal risk-sharing to buffer income shocks. Two types of behavior with regard to private monetary transfers are explicitly distinguished: (1) all households provide transfers whenever they can afford it and (2) insured households do not show solidarity with their uninsured peers.
The model is stylized and is not used to analyze a particular case study, but represents conditions from several regions with different risk contexts where informal risk-sharing networks between smallholder farmers are prevalent.
…
Netlogo Profiler code example
Colin Wren | Published Wednesday, March 04, 2015This is a very simple foraging model used to illustrate the features of Netlogo’s Profiler extension.
A discrete-time stochastic model with state-dependent transmission probabilities and multi-agent simulations focusing on possible risks that could materialize in the final phase of the epidemic.
Demand Planning Model
Iris Lorscheid Jonas Hauke Matthias Meyer | Published Wednesday, October 04, 2017Demand planning requires processing of distributed information. In this process, individuals, their properties and interactions play a crucial role. This model is a computational testbed to investigate these aspects with respect to forecast accuracy.
A model of circular migration
Anna Klabunde | Published Wednesday, August 07, 2013 | Last modified Wednesday, February 17, 2016An empirically validated agent-based model of circular migration
Displaying 10 of 487 results for "Tim M Daw" clear search