This package implements a simplified artificial agent-based demographic model of the UK. Individuals of an initial population are subject to ageing, deaths, births, divorces and marriages. A specific case-study simulation is progressed with a user-defined simulation fixed step size on a hourly, daily, weekly, monthly basis or even an arbitrary user-defined clock rate. While the model can serve as a base model to be adjusted to realistic large-scale socio-economics, pandemics or social interactions-based studies mainly within a demographic context, the main purpose of the model is to explore and exploit capabilities of the state-of-the-art Agents.jl Julia package as well as other ecosystem of Julia packages like GlobalSensitivity.jl. Code includes examples for evaluating global sensitivity analysis using Morris and Sobol methods and local sensitivity analysis using OFAT and OAT methods. Multi-threaded parallelization is enabled for improved runtime performance.

Country-by-Country Reporting and Automatic Exchange of Information have recently been implemented in European Union (EU) countries. These international tax reforms increase tax compliance in the short term. In the long run, however, taxpayers will continue looking abroad to avoid taxation and, countries, looking for additional revenues, will provide opportunities. As a result, tax competition intensifies and the initial increase in compliance could reverse. To avoid international tax reforms being counteracted by tax competition, this paper suggests bilateral responsive regulation to maximize compliance. This implies that countries would use different tax policy instruments toward other countries, including tax and secrecy havens.

To assess the effectiveness of fully or partially enforce tax policies, this agent based model has been ran many times under different enforcement rules, which influence the perceived enforced- and voluntary compliance, as the slippery-slope model prescribes. Based on the dynamics of this perception and the extent to which agents influence each other, the annual amounts of tax evasion, tax avoidance and taxes paid are calculated over longer periods of time.

The agent-based simulation finds that a differentiated policy response could increase tax compliance by 6.54 percent, which translates into an annual increase of €105 billion in EU tax revenues on income, profits, and capital gains. Corporate income tax revenues in France, Spain, and the UK alone would already account for €35 billion.

Viable North Sea (ViNoS) is an Agent-based Model of the German North Sea Small-scale Fisheries in a Social-Ecological Systems framework focussing on the adaptive behaviour of fishers facing regulatory, economic, and resource changes. Small-scale fisheries are an important part both of the cultural perception of the German North Sea coast and of its fishing industry. These fisheries are typically family-run operations that use smaller boats and traditional fishing methods to catch a variety of bottom-dwelling species, including plaice, sole, and brown shrimp. Fisheries in the North Sea face area competition with other uses of the sea – long practiced ones like shipping, gas exploration and sand extractions, and currently increasing ones like marine protection and offshore wind farming. German authorities have just released a new maritime spatial plan implementing the need for 30% of protection areas demanded by the United Nations High Seas Treaty and aiming at up to 70 GW of offshore wind power generation by 2045. Fisheries in the North Sea also have to adjust to the northward migration of their established resources following the climate heating of the water. And they have to re-evaluate their economic balance by figuring in the foreseeable rise in oil price and the need for re-investing into their aged fleet.

Package for simulating the behavior of experts in a scientific-forecasting competition, where the outcome of experiments itself depends on expert consensus. We pay special attention to the interplay between expert bias and trust in the reward algorithm. The package allows the user to reproduce results presented in arXiv:2305.04814, as well as testing of other different scenarios.

The first simple movement models used unbiased and uncorrelated random walks (RW). In such models of movement, the direction of the movement is totally independent of the previous movement direction. In other words, at each time step the direction, in which an individual is moving is completely random. This process is referred to as a Brownian motion.
On the other hand, in correlated random walks (CRW) the choice of the movement directions depends on the direction of the previous movement. At each time step, the movement direction has a tendency to point in the same direction as the previous one. This movement model fits well observational movement data for many animal species.

The presented agent based model simulated the movement of the agents as a correlated random walk (CRW). The turning angle at each time step follows the Von Mises distribution with a ϰ of 10. The closer ϰ gets to zero, the closer the Von Mises distribution becomes uniform. The larger ϰ gets, the more the Von Mises distribution approaches a normal distribution concentrated around the mean (0°).
In this script the turning angles (following the Von Mises distribution) are generated based on the the instructions from N. I. Fisher 2011.
This model is implemented in Javascript and can be used as a building block for more complex agent based models that would rely on describing the movement of individuals with CRW.

This is NetLogo code that presents two alternative implementations of Correlated Random Walk (CRW):
- 1. drawing the turning angles from the uniform distribution, i.e. drawing the angle with the same probability from a certain given range;
- 2. drawing the turning angles from von Mises distribution.
The move lengths are drawn from the lognormal distribution with the specified parameters.

Correlated Random Walk is used to represent the movement of animal individuals in two-dimensional space. When modeled as CRW, the direction of movement at any time step is correlated with the direction of movement at the previous time step. Although originally used to describe the movement of insects, CRW was later shown to sufficiently well describe the empirical movement data of other animals, such as wild boars, caribous, sea stars.
…

Confirmation Bias is usually seen as a flaw of the human mind. However, in some tasks, it may also increase performance. Here, agents are confronted with a number of binary Signals (A, or B). They have a base detection rate, e.g. 50%, and after they detected one signal, they get biased towards this type of signal. This means, that they observe that kind of signal a bit better, and the other signal a bit worse. This is moderated by a variable called “bias_effect”, e.g. 10%. So an agent who detects A first, gets biased towards A and then improves its chance to detect A-signals by 10%. Thus, this agent detects A-Signals with the probability of 50%+10% = 60% and detects B-Signals with the probability of 50%-10% = 40%.
Given such a framework, agents that have the ability to be biased have better results in most of the scenarios.

The model presented here is extensively described in the paper ‘Talk less to strangers: How homophily can improve collective decision-making in diverse teams’ (forthcoming at JASSS). A full replication package reproducing all results presented in the paper is accessible at https://osf.io/76hfm/.

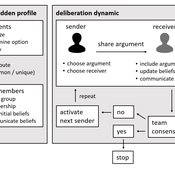
Narrative documentation includes a detailed description of the model, including a schematic figure and an extensive representation of the model in pseudocode.

The model develops a formal representation of a diverse work team facing a decision problem as implemented in the experimental setup of the hidden-profile paradigm. We implement a setup where a group seeks to identify the best out of a set of possible decision options. Individuals are equipped with different pieces of information that need to be combined to identify the best option. To this end, we assume a team of N agents. Each agent belongs to one of M groups where each group consists of agents who share a common identity.
The virtual teams in our model face a decision problem, in that the best option out of a set of J discrete options needs to be identified. Every team member forms her own belief about which decision option is best but is open to influence by other team members. Influence is implemented as a sequence of communication events. Agents choose an interaction partner according to homophily h and take turns in sharing an argument with an interaction partner. Every time an argument is emitted, the recipient updates her beliefs and tells her team what option she currently believes to be best. This influence process continues until all agents prefer the same option. This option is the team’s decision.

We present a socio-epistemic model of science inspired by the existing literature on opinion dynamics. In this model, we embed the agents (or scientists) into social networks - e.g., we link those who work in the same institutions. And we place them into a regular lattice - each representing a unique mental model. Thus, the global environment describes networks of concepts connected based on their similarity. For instance, we may interpret the neighbor lattices as two equivalent models, except one does not include a causal path between two variables.

Agents interact with one another and move across the epistemic lattices. In other words, we allow the agents to explore or travel across the mental models. However, we constrain their movements based on absorptive capacity and cognitive coherence. Namely, in each round, an agent picks a focal point - e.g., one of their colleagues - and will move towards it. But the agents’ ability to move and speed depends on how far apart they are from the focal point - and if their new position is cognitive/logic consistent.

Therefore, we propose an analytical model that examines the connection between agents’ accumulated knowledge, social learning, and the span of attitudes towards mental models in an artificial society. While we rely on the example from the General Theory of Relativity renaissance, our goal is to observe what determines the creation and diffusion of mental models. We offer quantitative and inductive research, which collects data from an artificial environment to elaborate generalized theories about the evolution of science.

Scholars have written extensively about hierarchical international order, on the one hand, and war on the other, but surprisingly little work systematically explores the connection between the two. This disconnect is all the more striking given that empirical studies have found a strong relationship between the two. We provide a generative computational network model that explains hierarchy and war as two elements of a larger recursive process: The threat of war drives the formation of hierarchy, which in turn shapes states’ incentives for war. Grounded in canonical theories of hierarchy and war, the model explains an array of known regularities about hierarchical order and conflict. Surprisingly, we also find that many traditional results of the IR literature—including institutional persistence, balancing behavior, and systemic self-regulation—emerge from the interplay between hierarchy and war.