About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 202 results behavior clear search
Proof of principle for a self-governing prediction and forecasting reward algorithm: Modeling consensus of a group of experts in adversarial collaboration.
Jose Osvaldo Gonzalez Hernandez Ted C. Rogers Jonathan Marino Brandon Velasco | Published Sunday, May 14, 2023Package for simulating the behavior of experts in a scientific-forecasting competition, where the outcome of experiments itself depends on expert consensus. We pay special attention to the interplay between expert bias and trust in the reward algorithm. The package allows the user to reproduce results presented in arXiv:2305.04814, as well as testing of other different scenarios.
Agent based modeling of the effects of carbon payments and forest owner cooperatives on carbon storage and revenue in Pacific Northwest forestlands.
Dan Brown Pranab Roy Chowdhury | Published Tuesday, May 09, 2023The Olympic Peninsula ABM works as a virtual laboratory to simulate the existing forestland management practices as followed by different forestland owner groups in the Olympic Peninsula, Washington, and explore how they could shape the future provisions of multifunctional ecosystem services such as Carbon storage and revenue generation under the business-as-usual scenario as well as by their adaptation to interventions. Forestlands are socio-ecological systems that interact with economic, socio-cultural, and policy systems. Two intervention scenarios were introduced in this model to simulate the adaptation of landowner behavior and test the efficacy of policy instruments in promoting sustainable forest practices and fostering Carbon storage and revenue generation. (1) A market-linked carbon offset scheme that pays the forestland owners a financial incentive in the form of a yearly carbon rent. (2) An institutional intervention policy that allows small forest owners (SFLO) to cooperate for increased market access and benefits under carbon rent scenario. The model incorporates the heterogeneous contexts within which the forestland owners operate and make their forest management decisions by parameterizing relevant agent attributes and contextualizing their unique decision-making processes.
An Agent Based Model of International Capital Flows
Harvey Baldovino | Published Thursday, April 06, 2023This is a preliminary attempt in creating an Agent-Based Model of capital flows. This is based on the theory of capital flows based on interest-rate differentials. Foreign capital flows to a country with higher interest rates relative to another. The model shows how capital volatilty and wealth concentration are affected by the speed of capital flow, number of investors, magnitude of changes in interest rate due to capital flows and the interest differential threshold that investors set in deciding whether to move capital or not. Investors in the model are either “regional” investors (only investing in neighboring countries) and “global” investors (those who invest anywhere in the world).
In the future, the author hopes to extend this model to incorporate capital flow based on changes in macroeconomic fundamentals, exchange rate volatility, behavioral finance (for instance, herding behavior) and the presence of capital controls.
Scholars have written extensively about hierarchical international order, on the one hand, and war on the other, but surprisingly little work systematically explores the connection between the two. This disconnect is all the more striking given that empirical studies have found a strong relationship between the two. We provide a generative computational network model that explains hierarchy and war as two elements of a larger recursive process: The threat of war drives the formation of hierarchy, which in turn shapes states’ incentives for war. Grounded in canonical theories of hierarchy and war, the model explains an array of known regularities about hierarchical order and conflict. Surprisingly, we also find that many traditional results of the IR literature—including institutional persistence, balancing behavior, and systemic self-regulation—emerge from the interplay between hierarchy and war.
Anxiety-to-Approach Agent-Based Model (Netlogo)
Marie Lisa Kogler | Published Tuesday, April 04, 2023An Agent-Based Model to simulate agent reactions to threatening information based on the anxiety-to-approach framework of Jonas et al. (2014).
The model showcases the framework of BIS/BAS (inhibitory and approach motivated behavior) for the case of climate information, including parameters for anxiety, environmental awareness, climate scepticism and pro-environmental behavior intention.
Agents receive external information according to threat-level and information frequency. The population dynamic is based on the learning from that information as well as social contagion mechanisms through a scale-free network topology.
The model uses Netlogo 6.2 and the network extension.
…
Knowledge Sharing in a Hospital
bpint Emily Molfino Joshua Goldstein Kathryn Schaefer Ziemer Mark Orr Bryan Lewis Jose Jimenez | Published Friday, January 27, 2023Organizations are complex systems comprised of many dynamic and evolving interaction patterns among individuals and groups. Understanding these interactions and how patterns, such as informal structures and knowledge sharing behavior, emerge are crucial to creating effective and efficient organizations. To explore such organizational dynamics, the agent-based model integrates a cognitive model, dynamic social networks, and a physical environment.
Peer reviewed Share: bottom-up disaster information management
Vittorio Nespeca Tina Comes Frances Brazier | Published Monday, December 05, 2022This model is intended to study the way information is collectively managed (i.e. shared, collected, processed, and stored) in a system and how it performs during a crisis or disaster. Performance is assessed in terms of the system’s ability to provide the information needed to the actors who need it when they need it. There are two main types of actors in the simulation, namely communities and professional responders. Their ability to exchange information is crucial to improve the system’s performance as each of them has direct access to only part of the information they need.
In a nutshell, the following occurs during a simulation. Due to a disaster, a series of randomly occurring disruptive events takes place. The actors in the simulation need to keep track of such events. Specifically, each event generates information needs for the different actors, which increases the information gaps (i.e. the “piles” of unaddressed information needs). In order to reduce the information gaps, the actors need to “discover” the pieces of information they need. The desired behavior or performance of the system is to keep the information gaps as low as possible, which is to address as many information needs as possible as they occur.
Peer reviewed Modelling Agricultural Innovations as a Social-Ecological Phenomenon
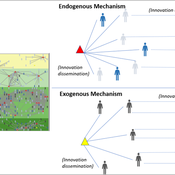
Maja Schlüter Udita Sanga | Published Thursday, November 17, 2022The goal of the AG-Innovation agent-based model is to explore and compare the effects of two alternative mechanisms of innovation development and diffusion (exogenous, linear and endogenous, non-linear) on emergent properties of food and income distribution and adoption rates of different innovations. The model also assesses the range of conditions under which these two alternative mechanisms would be effective in improving food security and income inequality outcomes. Our modelling questions were: i) How do cross-scalar social-ecological interactions within agricultural innovation systems affect system outcomes of food security and income inequality? ii) Do foreign aid-driven exogenous innovation perpetuate income inequality and food insecurity and if so, under which conditions? iii) Do community-driven endogenous innovations improve food security and income inequality and if so, under which conditions? The Ag-Innovation model is intended to serve as a thinking tool for for the development and testing of hypotheses, generating an understanding of the behavior of agricultural innovation systems, and identifying conditions under which alternated innovation mechanisms would improve food security and income inequality outcomes.
Household Energy Retrofit Behavior (HERB) ABM
Lars Even Egner | Published Thursday, October 20, 2022The HERB model simulates the retrofit behavior of homeowners in a neighborhood. The model initially parameterizes a neighborhood and households with technical factors such as energy standard, the availability of subsidies, and neighbors’ retrofit activity. Then, these factors are translated into psychological variables such as perceived comfort gain, worry about affording the retrofit, and perceiving the current energy standard of the home as wasteful. These psychological variables moderate the transition between four different stages of deciding to retrofit, as suggested by a behavioral model specific to household energy retrofitting identified based on a large population survey in Norway. The transition between all stages eventually leads to retrofitting, which affects both the household’s technical factors and friends and neighbors, bringing the model “full circle”. The model assumes that the energy standard of the buildings deteriorates over time, forcing households to retrofit regularly to maintain a certain energy standard.
Because experiment datafiles are about 15GB, they are available at https://doi.org/10.18710/XOSAMD
Communication and Trust in a Commons Dilemma Experiment
Marco Janssen | Published Sunday, October 02, 2022An agent model is presented that aims to capture the impact of cheap talk on collective action in a commons dilemma. The commons dilemma is represented as a spatially explicit renewable resource. Agent’s trust in others impacts the speed and harvesting rate, and trust is impacted by observed harvesting behavior and cheap talk. We calibrated the model using experimental data (DeCaro et al. 2021). The best fit to the data consists of a population with a small frequency of altruistic and selfish agents, and mostly conditional cooperative agents sensitive to inequality and cheap talk. This calibrated model provides an empirical test of the behavioral theory of collective action of Elinor Ostrom and Humanistic Rational Choice Theory.
Displaying 10 of 202 results behavior clear search