About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 990 results for "Chantal van Esch" clear search
Agent-based model of sexual partnership
Andrea Knittel | Published Monday, December 05, 2011 | Last modified Saturday, April 27, 2013In this model agents meet, evaluate one another, decide whether or not to date, if and when to become sexual partners, and when to break up.
Animal territory formation (Reusable Building Block RBB)
Volker Grimm Stephanie Kramer-Schadt Robert Zakrzewski | Published Sunday, November 12, 2023This is a generic sub-model of animal territory formation. It is meant to be a reusable building block, but not in the plug-and-play sense, as amendments are likely to be needed depending on the species and region. The sub-model comprises a grid of cells, reprenting the landscape. Each cell has a “quality” value, which quantifies the amount of resources provided for a territory owner, for example a tiger. “Quality” could be prey density, shelter, or just space. Animals are located randomly in the landscape and add grid cells to their intial cell until the sum of the quality of all their cells meets their needs. If a potential new cell to be added is owned by another animal, competition takes place. The quality values are static, and the model does not include demography, i.e. mortality, mating, reproduction. Also, movement within a territory is not represented.
Peer reviewed Family Herd Demography
Mark Moritz Ian M Hamilton Andrew Yoak Rebecca Garabed Abigail Buffington | Published Monday, August 15, 2016 | Last modified Saturday, January 06, 2018The model examines the dynamics of herd growth in African pastoral systems. We used it to examine the role of scale (herd size) stochasticity (in mortality, fertility, and offtake) on herd growth.
Communication and social change in space and time
Sebastian Kluesener Francesco Scalone Martin Dribe | Published Tuesday, May 17, 2016 | Last modified Friday, October 13, 2017This agent-based model simulates the diffusion of a social change process stratified by social class in space and time which is solely driven social and spatial variation in communication links.
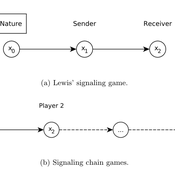
Lewis' Signaling Chains
Giorgio Gosti | Published Wednesday, January 14, 2015 | Last modified Friday, April 03, 2015Signaling chains are a special case of Lewis’ signaling games on networks. In a signaling chain, a sender tries to send a single unit of information to a receiver through a chain of players that do not share a common signaling system.
Artificial Long House Valley-Black Mesa
Lisa Sattenspiel Amy Warren | Published Thursday, March 19, 2020This model is an extension of the Artificial Long House Valley (ALHV) model developed by the authors (Swedlund et al. 2016; Warren and Sattenspiel 2020). The ALHV model simulates the population dynamics of individuals within the Long House Valley of Arizona from AD 800 to 1350. Individuals are aggregated into households that participate in annual agricultural and demographic cycles. The present version of the model incorporates features of the ALHV model including realistic age-specific fertility and mortality and, in addition, it adds the Black Mesa environment and population, as well as additional methods to allow migration between the two regions.
As is the case for previous versions of the ALHV model as well as the Artificial Anasazi (AA) model from which the ALHV model was derived (Axtell et al. 2002; Janssen 2009), this version makes use of detailed archaeological and paleoenvironmental data from the Long House Valley and the adjacent areas in Arizona. It also uses the same methods as the original AA model to estimate annual maize productivity of various agricultural zones within the Long House Valley. A new environment and associated methods have been developed for Black Mesa. Productivity estimates from both regions are used to determine suitable locations for households and farms during each year of the simulation.
The Travel-tour case study
Christophe Sibertin-Blanc Françoise Adreit Joseph El Gemayel | Published Sunday, May 19, 2013 | Last modified Friday, June 14, 2013This model describes and analyses the Travel-Tour Case study.
A Bottom-Up Simulation on Competition and Displacement of Online Interpersonal Communication Platforms
great-sage-futao | Published Tuesday, December 31, 2019 | Last modified Tuesday, December 31, 2019This model aims to simulate Competition and Displacement of Online Interpersonal Communication Platforms process from a bottom-up angle. Individual interpersonal communication platform adoption and abandonment serve as the micro-foundation of the simulation model. The evolution mode of platform user online communication network determines how present platform users adjust their communication relationships as well as how new users join that network. This evolution mode together with innovations proposed by individual interpersonal communication platforms would also have impacts on the platform competition and displacement process and result by influencing individual platform adoption and abandonment behaviors. Three scenes were designed to simulate some common competition situations occurred in the past and current time, that two homogeneous interpersonal communication platforms competed with each other when this kind of platforms first came into the public eye, that a late entrant platform with a major innovation competed with the leading incumbent platform during the following days, as well as that both the leading incumbent and the late entrant continued to propose many small innovations to compete in recent days, respectively.
Initial parameters are as follows: n(Nmax in the paper), denotes the final node number of the online communication network node. mi (m in the paper), denotes the initial degree of those initial network nodes and new added nodes. pc(Pc in the paper), denotes the proportion of links to be removed and added in each epoch. pst(Pv in the paper), denotes the proportion of nodes with a viscosity to some platforms. comeintime(Ti in the paper), denotes the epoch when Platform 2 joins the market. pit(Pi in the paper), denotes the proportion of nodes adopting Platform 2 immediately at epoch comeintime(Ti). ct(Ct in the paper), denotes the Innovation Effective Period length. In Scene 2, There is only one major platform proposed by Platform 2, and ct describes that length. However, in Scene 3, Platform 2 and 1 will propose innovations alternately. And so, we set ct=10000 in simulation program, and every jtt epochs, we alter the innovation proposer from one platform to the other. Hence in this scene, jtt actually denotes the Innovation Effective Period length instead of ct.
Digital divide and opinion formation
Dongwon Lim | Published Friday, November 02, 2012 | Last modified Monday, May 20, 2013This model extends the bounded confidence model of Deffuant and Weisbuch. It introduces online contexts in which a person can deliver his or her opinion to several other persons. There are 2 additional parameters accessibility and connectivity.
cultural group and persistent parochialism
Jae-Woo Kim | Published Monday, November 08, 2010 | Last modified Saturday, April 27, 2013Discriminators who have limited tolerance for helping dissimilar others are necessary for the evolution of costly cooperation in a one-shot Prisoner’s Dilemma. Existing research reports that trust in
Displaying 10 of 990 results for "Chantal van Esch" clear search