About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 332 results for "Ali Termos" clear search
Ant Colony Optimization for infrastructure routing
Igor Nikolic Emile Chappin P W Heijnen | Published Wednesday, March 05, 2014 | Last modified Saturday, March 24, 2018The mode implements a variant of Ant Colony Optimization to explore routing on infrastructures through a landscape with forbidden zones, connecting multiple sinks to one source.
06b EiLab_Model_I_V5.00 NL
Garvin Boyle | Published Saturday, October 05, 2019EiLab - Model I - is a capital exchange model. That is a type of economic model used to study the dynamics of modern money which, strangely, is very similar to the dynamics of energetic systems. It is a variation on the BDY models first described in the paper by Dragulescu and Yakovenko, published in 2000, entitled “Statistical Mechanics of Money”. This model demonstrates the ability of capital exchange models to produce a distribution of wealth that does not have a preponderance of poor agents and a small number of exceedingly wealthy agents.
This is a re-implementation of a model first built in the C++ application called Entropic Index Laboratory, or EiLab. The first eight models in that application were labeled A through H, and are the BDY models. The BDY models all have a single constraint - a limit on how poor agents can be. That is to say that the wealth distribution is bounded on the left. This ninth model is a variation on the BDY models that has an added constraint that limits how wealthy an agent can be? It is bounded on both the left and right.
EiLab demonstrates the inevitable role of entropy in such capital exchange models, and can be used to examine the connections between changing entropy and changes in wealth distributions at a very minute level.
…
FlowLogo: An agent-based platform for simulating complex human-aquifer interactions in managed groundwater systems
Juan Castilla-Rho | Published Sunday, August 30, 2015FlowLogo integrates agent-based and groundwater flow simulation. It aims to simplify the process of developing participatory ABMs in the groundwater space and begin the exploration of novel, bottom-up solutions to conflicts in shared aquifers.
The role of spatial foresight in models of hominin dispersal
Colin Wren | Published Monday, February 24, 2014 | Last modified Monday, July 14, 2014The natural selection of foresight, an accuracy at assess the environment, under degrees of environmental heterogeneity. The model is designed to connect local scale mobility, from foraging, with the global scale phenomenon of population dispersal.
Foundress dilemma model
Marco Janssen Takao Sasaki Zachary Joseph Shaffer Stephen Pratt Brian Haney Jennifer Fewell | Published Thursday, July 28, 2016A haystack-style model of group selection to capture the essential features of colony foundation for queens of the ant based on observation of the ant Pogonomyrmex californicus.
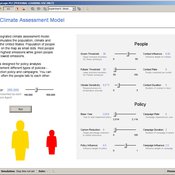
HCAM: A Hybrid Climate Assessment Model
Peer-Olaf Siebers | Published Wednesday, November 06, 2019This model is part of a JASSS article that introduce a conceptual framework for developing hybrid (system dynamics and agent-based) integrated assessment models, which focus on examining the human impacts on climate change. This novel modelling approach allows to reuse existing rigid, but well-established integrated assessment models, and adds more flexibility by replacing aggregate stocks with a community of vibrant interacting entities. The model provides a proof-of-concept of the application of this conceptual framework in form of an illustrative example. taking the settings of the US. It is solely created for the purpose of demonstrating our hybrid modelling approach; we do not claim that it has predictive powers.
Coastal Coupled Housing and Land Markets (C-CHALMS)
Nicholas Magliocca | Published Thursday, May 18, 2017Next generation of the CHALMS model applied to a coastal setting to investigate the effects of subjective risk perception and salience decision-making on adaptive behavior by residents.
Social Identity Model of Protest Emergence (SIMPE)
Cristina Chueca Del Cerro | Published Friday, March 17, 2023The Social Identity Model of Protest Emergence (SIMPE), an agent-based model of national identity and protest mobilisations.
I developed this model for my PhD project, “Polarisation and Protest Mobilisation Around Secessionist Movements: an Agent-Based Model of Online and Offline Social Networks”, at the University of Glasgow (2019-2023).
The purpose of this model is to simulate protest emergence in a given country where there is an independence movement, fostering the self-categorisation process of national identification. In order to contextualised SIMPE, I have used Catalonia, where an ongoing secessionist movement since 2011 has been present, national identity has shown signs of polarisation, and where numerous mobilisations have taken place over the last decade. Data from the Catalan Centre of Opinion Studies (CEO) has been used to inform some of the model parameters.
…
Interactions between organizations and social networks in common-pool resource governance
Phesi Project | Published Monday, October 29, 2012 | Last modified Saturday, April 27, 2013Explores how social networks affect implementation of institutional rules in a common pool resource.
Social identity approach in a data-driven Axelrod model
alejandrodinkelberg | Published Thursday, July 28, 2022Simulations based on the Axelrod model and extensions to inspect the volatility of the features over time (AXELROD MODEL & Agreement threshold & two model variations based on the Social identity approach)
The Axelrod model is used to predict the number of changes per feature in comparison to the datasets and is used to compare different model variations and their performance.
Input: Real data
…
Displaying 10 of 332 results for "Ali Termos" clear search