About the CoMSES Model Library more info
Our mission is to help computational modelers at all levels engage in the establishment and adoption of community standards and good practices for developing and sharing computational models. Model authors can freely publish their model source code in the Computational Model Library alongside narrative documentation, open science metadata, and other emerging open science norms that facilitate software citation, reproducibility, interoperability, and reuse. Model authors can also request peer review of their computational models to receive a DOI.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with additional detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 132 results evolution clear search
Peer reviewed ACross (Academic Collaboration, Research, Output, and System Simulation)
Wenhan Feng Bayi Li | Published Saturday, June 28, 2025The primary purpose of this model is to explain the dynamic processes within university-centered collaboration networks, with a particular focus on the complex transformation of academic knowledge into practical projects. Based on investigations of actual research projects and a thorough literature review, the model integrates multiple drivers and influencing factors to explore how these factors affect the formation and evolution of collaboration networks under different parameter scenarios. The model places special emphasis on the impact of disciplinary attributes, knowledge exchange, and interdisciplinary collaboration on the dynamics of collaboration networks, as well as the complex mechanisms of network structure, system efficiency, and interdisciplinary interactions during project formation.
Specifically, the model aims to:
- Simulate how university research departments drive the formation of research projects through knowledge creation.
- Investigate how the dynamics of collaboration networks influence the transformation of innovative hypotheses into matured projects.
- Examine the critical roles of knowledge exchange and interdisciplinary collaboration in knowledge production and project formation.
- Provide both quantitative and qualitative insights into the interactions among academia, industry, and project outputs.
Development of coral reefs under climate change impacts and adaptation options
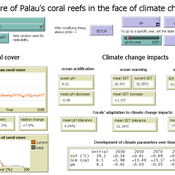
Nina Preußler | Published Friday, May 30, 2025This NetLogo model simulates how coral reefs around the islands of Palau would develop under different emission scenarios and with selected adaptation strategies. Reef health is indicated by coral cover (%) and is affected by four major climate change impacts: increasing sea surface temperature, sea level rise, ocean acidification, and more intense typhoons. The model differentiates between inner and outer reefs, with the former naturally adapted to warmer, more acidic waters. The simulation includes bleaching events and possible recovery. In addition, the user can choose between different coral transplantation strategies as well as regulate natural thermal adaptation rates.
Gaming Polarisation: Using Agent-Based Simulations as A Dialogue Tool
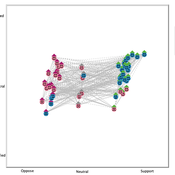
Shaoni Wang | Published Friday, May 09, 2025This model aims to replicate the evolution of opinions and behaviours on a communal plan over time. It also aims to foster community dialogue on simulation outcomes, promoting inclusivity and engagement. Individuals (referred to as agents), grouped based on Sinus Milieus (Groh-Samberg et al., 2023), face a binary choice: support or oppose the plan. Motivated by experiential, social, and value needs (Antosz et al., 2019), their decision is influenced by how well the plan aligns with these fundamental needs.
Peer reviewed Evolution of Conditional Cooperation in a Spatial Public Goods Game
Marco Janssen Francesca Federico Raksha Balakrishna | Published Saturday, March 15, 2025A model to investigate the Evolution of Conditional Cooperation in a Spatial Public Goods Game. We consider two conditional cooperation strategies: one based on thresholds (Battu & Srinivasan, 2020) and another based on independent decisions for each number of cooperating neighbors. We examine the effects of productivity and conditional cooperation criteria on the trajectory of cooperation. Cooperation is evolving with no need for additional mechanisms apart from spatial structure when agents follow conditional strategies. We confirm the positive influence of productivity and cluster formation on the evolution of cooperation in spatial models. Results are robust for the two types of conditional cooperation strategies.
Peer reviewed Environmental stochasticity, resource heterogeneity, and the evolution of cooperation
Colin Lynch Carl Lipo Terry Hunt Michaela Starkey | Published Friday, March 14, 2025 | Last modified Tuesday, July 08, 2025The emergence of cooperation in human societies is often linked to environmental constraints, yet the specific conditions that promote cooperative behavior remain an open question. This study examines how resource unpredictability and spatial dispersion influence the evolution of cooperation using an agent-based model (ABM). Our simulations test the effects of rainfall variability and resource distribution on the survival of cooperative and non-cooperative strategies. The results show that cooperation is most likely to emerge when resources are patchy, widely spaced, and rainfall is unpredictable. In these environments, non-cooperators rapidly deplete local resources and face high mortality when forced to migrate between distant patches. In contrast, cooperators—who store and share resources—can better endure extended droughts and irregular resource availability. While rainfall stochasticity alone does not directly select for cooperation, its interaction with resource patchiness and spatial constraints creates conditions where cooperative strategies provide a survival advantage. These findings offer broader insights into how environmental uncertainty shapes social organization in resource-limited settings. By integrating ecological constraints into computational modeling, this study contributes to a deeper understanding of the conditions that drive cooperation across diverse human and animal systems.
Cultural transmission in structured populations
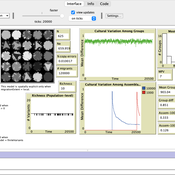
Luke Premo | Published Wednesday, November 13, 2024This structured population model is built to address how migration (or intergroup cultural transmission), copying error, and time-averaging affect regional variation in a single selectively neutral discrete cultural trait under different mechanisms of cultural transmission. The model allows one to quantify cultural differentiation between groups within a structured population (at equilibrium) as well as between regional assemblages of time-averaged archaeological material at two different temporal scales (1,000 and 10,000 ticks). The archaeological assemblages begin to accumulate only after a “burn-in” period of 10,000 ticks. The model includes two different representations of copying error: the infinite variants model of copying error and the finite model of copying error. The model also allows the user to set the variant ceiling value for the trait in the case of the finite model of copying error.
Blending vs particulate inheritance - demo of Fisher (1930)
Paul Smaldino | Published Friday, September 13, 2024A simple model illustrating RA Fisher’s (1930) reconciliation of Darwinian selection with particulate genetic contributions.
GODS: Gossip-Oriented Dilemma Simulator
Jan Majewski | Published Wednesday, September 04, 2024Model of influence of access to social information spread via social network on decisions in a two-person game.
EU language skills
Marco Civico | Published Sunday, July 07, 2024The objective of this agent-based model is to test different language education orientations and their consequences for the EU population in terms of linguistic disenfranchisement, that is, the inability of citizens to understand EU documents and parliamentary discussions should their native language(s) no longer be official. I will focus on the impact of linguistic distance and language learning. Ideally, this model would be a tool to help EU policy makers make informed decisions about language practices and education policies, taking into account their consequences in terms of diversity and linguistic disenfranchisement. The model can be used to force agents to make certain choices in terms of language skills acquisition. The user can then go on to compare different scenarios in which language skills are acquired according to different rationales. The idea is that, by forcing agents to adopt certain language learning strategies, the model user can simulate policies promoting the acquisition of language skills and get an idea of their impact. In this way the model allows not only to sketch various scenarios of the evolution of language skills among EU citizens, but also to estimate the level of disenfranchisement in each of these scenarios.
SeaROOTS ABM: Simulating Artificial Hominins Maritime Mobility at Inner Ionian, Greece
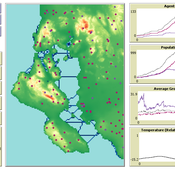
Angelos Chliaoutakis | Published Wednesday, May 29, 2024SeaROOTS ABM is a quite generic agent-based modeling system, for simulating and evaluating potential terrestrial and maritime mobility of artificial hominin groups, configured by available archaeological data and hypotheses. Necessary bathymetric, geomorphological and paleoenvironmental data are combined in order to reconstruct paleoshorelines for the study area and produce an archaeologically significant agent environment. Paleoclimatic and archaeological data are incorporated in the ABM in order to simulate maritime crossings and assess the emergent patterns of interaction between human agency and the sea.
SeaROOTS agent-based system includes completely autonomous, utility-based agents (Chliaoutakis & Chalkiadakis 2016), representing artificial hominin groups, with partial knowledge of their environment, for simulating their evolution and potential maritime mobility, utilizing alternative Least Cost Path analysis modeling techniques (Gustas & Supernant 2017, Gravel-Miguel & Wren 2021). Two groups of hominins, Neanderthals and Homo sapiens, are chosen in order to study the challenges and actions employed as a response to the fluctuating sea-levels, as well as probability scenarios with respect to sea-crossings via buoyant vessels (rafting) or the human body itself (swimming). SeaROOTS ABM aims to simulate various scenarios and investigate the degree climatic fluctuations influenced such activities and interactions in the Middle Paleolithic period.
The model focuses on simulating potential terrestrial and maritime routes, explore the interactions and relations between autonomous agents and their environment, as well as to test specific research questions; for example, when and under what conditions would Middle Paleolithic hominins be more likely to attempt a crossing and successfully reach the islands? By which agent type (Sapiens or Neanderthals) and how (e.g. swimming or by sea-vessels) could such short sea crossings be (mostly) attempted, and which (sea) routes were usually considered by the agents? When does a sea-crossing become a choice and when is it a result of forced migration, i.e. disaster- or conflict-induced displacement? Results show that the dynamic marine environment of the Inner Ionian, our case study in this work, played an important role in their decision-making process.
Displaying 10 of 132 results evolution clear search