About the CoMSES Model Library more info
Our mission is to help computational modelers at all levels engage in the establishment and adoption of community standards and good practices for developing and sharing computational models. Model authors can freely publish their model source code in the Computational Model Library alongside narrative documentation, open science metadata, and other emerging open science norms that facilitate software citation, reproducibility, interoperability, and reuse. Model authors can also request peer review of their computational models to receive a DOI.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with additional detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 133 results for "José I Santos" clear search
Vacunación-Covid Ecuador
Adrian Lara | Published Tuesday, March 22, 2022El modelo a continuación, fue desarrollado para el DATA CHALLENGE 2022. Es un análisis de la información descargada del Portal de datos abiertos de Ecuador. Dentro del modelo podemos realizar una breve exploración de la información así como una simulación respecto al proceso de vacunación en Ecuador.
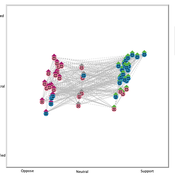
Gaming Polarisation: Using Agent-Based Simulations as A Dialogue Tool
Shaoni Wang | Published Friday, May 09, 2025This model aims to replicate the evolution of opinions and behaviours on a communal plan over time. It also aims to foster community dialogue on simulation outcomes, promoting inclusivity and engagement. Individuals (referred to as agents), grouped based on Sinus Milieus (Groh-Samberg et al., 2023), face a binary choice: support or oppose the plan. Motivated by experiential, social, and value needs (Antosz et al., 2019), their decision is influenced by how well the plan aligns with these fundamental needs.
An Agent-based Model of Firm Size Distribution and Collaborative Innovation
Inyoung Hwang | Published Monday, December 09, 2019I added a discounting rate to the equation for expected values of defective / collaborative strategies.
The discounting rate was set to 0.956, the annual average from 1980 to 2015, using the Consumer Price Index (CPI) of Statistics Korea.
WeDiG Sim
Reza Shamsaee | Published Monday, May 14, 2012 | Last modified Saturday, April 27, 2013WeDiG Sim- Weighted Directed Graph Simulator - is an open source application that serves to simulate complex systems. WeDiG Sim reflects the behaviors of those complex systems that put stress on scale-free, weightedness, and directedness. It has been implemented based on “WeDiG model” that is newly presented in this domain. The WeDiG model can be seen as a generalized version of “Barabási-Albert (BA) model”. WeDiG not only deals with weighed directed systems, but also it can handle the […]
A Double-Auction Equity Market For a Single Firm with AR1 Earnings
Eric Weisbrod | Published Monday, December 13, 2010 | Last modified Saturday, April 27, 2013This is a final project for the class AML 591 at Arizona State University. I have done a small amount of bug-checking, but overall the project represents only a half of a semester’s work, so proceed w
How to not get stuck – an ant model showing how negative feedback due to crowding maintains flexibility in ant foraging
Tomer Czaczkes | Published Thursday, December 17, 2015Positive feedback can lead to “trapping” in local optima. Adding a simple negative feedback effect, based on ant behaviour, prevents this trapping
Location Analysis Hybrid ABM
Lukasz Kowalski | Published Friday, February 08, 2019The purpose of this hybrid ABM is to answer the question: where is the best place for a new swimming pool in a region of Krakow (in Poland)?
The model is well described in ODD protocol, that can be found in the end of my article published in JASSS journal (available online: http://jasss.soc.surrey.ac.uk/22/1/1.html ). Comparison of this kind of models with spatial interaction ones, is presented in the article. Before developing the model for different purposes, area of interest or services, I recommend reading ODD protocol and the article.
I published two films on YouTube that present the model: https://www.youtube.com/watch?v=iFWG2Xv20Ss , https://www.youtube.com/watch?v=tDTtcscyTdI&t=1s
…
RobbyGA modified 2019
Timothy Gooding | Published Sunday, February 24, 2019This is a modification of the RobbyGA model by the Santa Fe Institute (see model Info tab for full information). The basic idea is that the GA has been changed to one where the agents have a set lifetime, anyone can reproduce with anyone, but where there is a user-set amount of ‘starvation’ that kills the agents that have a too low fitness.
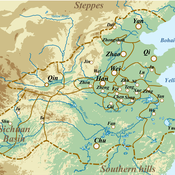
Evolutionary Dynamics of the Warring States Period: Initial Unification in Ancient China (475 BC to 221 BC)
zhuo zhang | Published Sunday, August 07, 2022If you have any questions about the model run, please send me an email and I will respond as soon as possible.
Under complex system perspectives, we build the multi-agent system to back-calculate this unification process of the Warring State period, from 32 states in 475 BC to 1 state (Qin) in 221 BC.
ABM Simulation of Transition from Late Longshan Cultures to Early Erlitou Culture
Carmen Iasiello | Published Sunday, November 26, 2023Within the archeological record for Bronze Age Chinese culture, there continues to be a gap in our understanding of the sudden rise of the Erlitou State from the previous late Longshan chiefdoms. In order to examine this period, I developed and used an agent-based model (ABM) to explore possible socio-politically relevant hypotheses for the gap between the demise of the late Longshan cultures and rise of the first state level society in East Asia. I tested land use strategy making and collective action in response to drought and flooding scenarios, the two plausible environmental hazards at that time. The model results show cases of emergent behavior where an increase in social complexity could have been experienced if a catastrophic event occurred while the population was sufficiently prepared for a different catastrophe, suggesting a plausible lead for future research into determining the life of the time period.
The ABM published here was originally developed in 2016 and its results published in the Proceedings of the 2017 Winter Simulation Conference.
Displaying 10 of 133 results for "José I Santos" clear search