About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 801 results for "Jon Norberg" clear search
Peer reviewed Gregarious Behavior, Human Colonization and Social Differentiation Agent-Based Model
Gert Jan Hofstede Mark R Kramer Sebastian Fajardo Andrés Bernal Martijn de Vries | Published Thursday, August 20, 2020 | Last modified Thursday, October 29, 2020Studies of colonization processes in past human societies often use a standard population model in which population is represented as a single quantity. Real populations in these processes, however, are structured with internal classes or stages, and classes are sometimes created based on social differentiation. In this present work, information about the colonization of old Providence Island was used to create an agent-based model of the colonization process in a heterogeneous environment for a population with social differentiation. Agents were socially divided into two classes and modeled with dissimilar spatial clustering preferences. The model and simulations assessed the importance of gregarious behavior for colonization processes conducted in heterogeneous environments by socially-differentiated populations. Results suggest that in these conditions, the colonization process starts with an agent cluster in the largest and most suitable area. The spatial distribution of agents maintained a tendency toward randomness as simulation time increased, even when gregariousness values increased. The most conspicuous effects in agent clustering were produced by the initial conditions and behavioral adaptations that increased the agent capacity to access more resources and the likelihood of gregariousness. The approach presented here could be used to analyze past human colonization events or support long-term conceptual design of future human colonization processes with small social formations into unfamiliar and uninhabited environments.
Human Environment Estuarine Systems Investigator
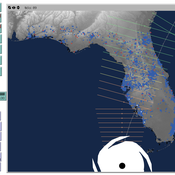
Andrew Allison | Published Friday, February 26, 2021This model simulates the form and function of an idealised estuary with associated barrier-spit complex on the north east coast of New Zealand’s North Island (from Bream Bay to central Bay of Plenty) during the years 2010 - 2050 CE. It combines variables from social, ecological and geomorphic systems to simulate potential directions of change in shallow coastal systems in response to external forcing from land use, climate, pollution, population density, demographics, values and beliefs. The estuary is over 1000Ha, making it a large estuary according to Hume et al. (2007) - there are 12 large estuaries in the Auckland region alone (Suyadi et al., 2019). The model was developed as part of Andrew Allison’s PhD Thesis in Geography from the School of Environment and Institute of Marine Science, University of Auckland, New Zealand. The model setup allows for alteration of geomorphic, ecological and social variables to suit the specific conditions found in various estuaries along the north east coast of New Zealand’s North Island.
This model is not a predictive or forecasting model. It is designed to investigate potential directions of change in complex shallow coastal systems. This model must not be used for any purpose other than as a heuristic to facilitate researcher and stakeholder learning and for developing system understanding (as per Allison et al., 2018).
Competitive Arousal Agent Based Model
Zoé Chollet | Published Friday, May 13, 2022What is it?
This model demonstrates a very simple bidding market where buyers try to acquire a desired item at the best price in a competitive environment
…
A stylized scale model to codesign with villagers an agent-based model of bushmeat hunting in the periphery of Korup National Park (Cameroon)
A Multi-level Multi-model of Collective Motion
Benjamin Camus Christine Bourjot Vincent Chevrier | Published Wednesday, March 25, 2015This multi-model (i.e. a model composed of interacting submodels) is a multi-level representation of a collective motion phenomenon. It was designed to study the impact of the mutual influences between individuals and groups in collective motion.
Composite Collective Decision Making - ant colony foraging model
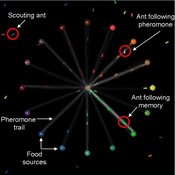
Tomer Czaczkes Benjamin I Czaczkes | Published Thursday, December 17, 2015The model explores how two types of information - social (in the form of pheromone trails) and private (in the form of route memories) affect ant colony level foraging in a variable enviroment.
Peer reviewed CHIME ABM Hurricane Evacuation Model
Joshua Watts | Published Friday, March 03, 2017 | Last modified Wednesday, May 29, 2019The CHIME ABM explores information distribution networks and agents’ protective decision making in the context of hurricane landfall.
Agent-based model of WiFi tracking system in urban environment
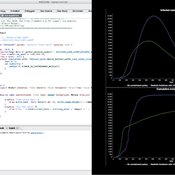
Christopher Thron Khoi Tran | Published Friday, April 21, 2017This code simulates the WiFi user tracking system described in: Thron et al., “Design and Simulation of Sensor Networks for Tracking Wifi Users in Outdoor Urban Environments”. Testbenches used to create the figures in the paper are included.
Peer reviewed Empathy & Power
J M Applegate Ned Wellman | Published Monday, November 13, 2017 | Last modified Thursday, December 21, 2017The purpose of this model is to explore the effects of different power structures on a cross-functional team’s prosocial decision making. Are certain power distributions more conducive to the team making prosocial decisions?
Peer reviewed COMOKIT
Patrick Taillandier Alexis Drogoul Benoit Gaudou Kevin Chapuis Nghi Huyng Quang Doanh Nguyen Ngoc Arthur Brugière Pierre Larmande Marc Choisy Damien Philippon | Published Tuesday, May 26, 2020 | Last modified Wednesday, July 01, 2020In the face of the COVID-19 pandemic, public health authorities around the world have experimented, in a short period of time, with various combinations of interventions at different scales. However, as the pandemic continues to progress, there is a growing need for tools and methodologies to quickly analyze the impact of these interventions and answer concrete questions regarding their effectiveness, range and temporality.
COMOKIT, the COVID-19 modeling kit, is such a tool. It is a computer model that allows intervention strategies to be explored in silico before their possible implementation phase. It can take into account important dimensions of policy actions, such as the heterogeneity of individual responses or the spatial aspect of containment strategies.
In COMOKIT, built using the agent-based modeling and simulation platform GAMA, the profiles, activities and interactions of people, person-to-person and environmental transmissions, individual clinical statuses, public health policies and interventions are explicitly represented and they all serve as a basis for describing the dynamics of the epidemic in a detailed and realistic representation of space.
…
Displaying 10 of 801 results for "Jon Norberg" clear search