About the CoMSES Model Library more info
Our mission is to help computational modelers at all levels engage in the establishment and adoption of community standards and good practices for developing and sharing computational models. Model authors can freely publish their model source code in the Computational Model Library alongside narrative documentation, open science metadata, and other emerging open science norms that facilitate software citation, reproducibility, interoperability, and reuse. Model authors can also request peer review of their computational models to receive a DOI.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with additional detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 11 results spatial distribution clear search
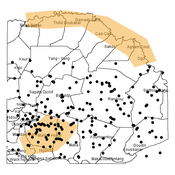
Agent-based modeling of the spatio-temporal distribution of Sahelian transhumant herds
Cheick Amed Diloma Gabriel TRAORE Etienne DELAY Alassane Bah Djibril Diop | Published Tuesday, May 20, 2025Sahelian transhumance is a seasonal pastoral mobility between the transhumant’s terroir of origin and one or more host terroirs. Sahelian transhumance can last several months and extend over hundreds of kilometers. Its purpose is to ensure efficient and inexpensive feeding of the herd’s ruminants. This paper describes an agent-based model to determine the spatio-temporal distribution of Sahelian transhumant herds and their impact on vegetation. Three scenarios based on different values of rainfall and the proportion of vegetation that can be grazed by transhumant herds are simulated. The results of the simulations show that the impact of Sahelian transhumant herds on vegetation is not significant and that rainfall does not impact the alley phase of transhumance. The beginning of the rainy season has a strong temporal impact on the spatial distribution of transhumant herds during the return phase of transhumance.
Sandy Beach Visitor Flow: An Agent-Based Model
Elham Bakhshianlamouki | Published Thursday, March 14, 2024The model is intended to simulate visitor spatial and temporal dynamics, encompassing their numbers, activities, and distribution along a coastline influenced by beach landscape design. Our primary focus is understanding how the spatial distribution of services and recreational facilities (e.g., beach width, entrance location, recreational facilities, parking availability) impacts visitation density. Our focus is not on tracking the precise visitation density but rather on estimating the areas most affected by visitor activity. This comprehension allows for assessing the diverse influences of beach layouts on spatial visitor density and, consequently, on the landscape’s biophysical characteristics (e.g., vegetation, fauna, and sediment features).
Peer reviewed Gregarious Behavior, Human Colonization and Social Differentiation Agent-Based Model
Gert Jan Hofstede Mark R Kramer Sebastian Fajardo Andrés Bernal Martijn de Vries | Published Thursday, August 20, 2020 | Last modified Thursday, October 29, 2020Studies of colonization processes in past human societies often use a standard population model in which population is represented as a single quantity. Real populations in these processes, however, are structured with internal classes or stages, and classes are sometimes created based on social differentiation. In this present work, information about the colonization of old Providence Island was used to create an agent-based model of the colonization process in a heterogeneous environment for a population with social differentiation. Agents were socially divided into two classes and modeled with dissimilar spatial clustering preferences. The model and simulations assessed the importance of gregarious behavior for colonization processes conducted in heterogeneous environments by socially-differentiated populations. Results suggest that in these conditions, the colonization process starts with an agent cluster in the largest and most suitable area. The spatial distribution of agents maintained a tendency toward randomness as simulation time increased, even when gregariousness values increased. The most conspicuous effects in agent clustering were produced by the initial conditions and behavioral adaptations that increased the agent capacity to access more resources and the likelihood of gregariousness. The approach presented here could be used to analyze past human colonization events or support long-term conceptual design of future human colonization processes with small social formations into unfamiliar and uninhabited environments.
Agent-based model for the socio-economic monitoring of visitor streams
Stefan Mohr | Published Saturday, January 20, 2018Due to the large extent of the Harz National Park, an accurate measurement of visitor numbers and their spatiotemporal distribution is not feasible. This model demonstrates the possibility to simulate the streams of visitors with ABM methodology.
Salzburg Bicycle model
Gudrun Wallentin | Published Saturday, October 29, 2016An ABM to simulate the spatio-temporal distribution of cyclists across the road network of the city of Salzburg.
The MOBILITY model analyzes how agents’ mobility affects the performance of social-ecological systems in different landscape configurations.
Peer reviewed AZOI: Another Zone Of Influence model
Cyril Piou | Published Wednesday, July 23, 2014 | Last modified Thursday, December 11, 2014This model reimplement Weiner et al. 2001 Zone Of Influence model to simulate plant growth under competition. The reimplementation in Netlogo and the ODD description in the “info” tab try to be as consistent as possible with the original paper.
ForagerNet3_Demography_V2
Andrew White | Published Thursday, February 13, 2014ForagerNet3_Demography_V2 is a non-spatial ABM for exploring hunter-gatherer demography. This version (developed from FN3D_V1) contains code for calculating the ratio of old to young adults (the “OY ratio”) in the living and dead populations.
Soil microbe-predator model with enzymes
Randall Boone John C Moore Akihiro Koyama Kirstin Holfelder | Published Thursday, November 21, 2013We seek to improve understanding of roles enzyme play in soil food webs. We created an agent-based simulation of a simple food web that includes enzymatic activity. The model was used in a publication, Moore et al. (in press; Biochemistry).
ForagerNet3_Demography: A Non-Spatial Model of Hunter-Gatherer Demography
Andrew White | Published Thursday, October 17, 2013 | Last modified Thursday, October 17, 2013ForagerNet3_Demography is a non-spatial ABM for exploring hunter-gatherer demography. Key methods represent birth, death, and marriage. The dependency ratio is an imporant variable in many economic decisions embedded in the methods.
Displaying 10 of 11 results spatial distribution clear search