About the CoMSES Model Library more info
Our mission is to help computational modelers at all levels engage in the establishment and adoption of community standards and good practices for developing and sharing computational models. Model authors can freely publish their model source code in the Computational Model Library alongside narrative documentation, open science metadata, and other emerging open science norms that facilitate software citation, reproducibility, interoperability, and reuse. Model authors can also request peer review of their computational models to receive a DOI.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with additional detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 71 results for "Emily Silver Huff" clear search
Private forest owner management behavior using social interactions, information flow, and peer-to-peer n
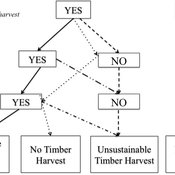
Jessica Leahy Emily Silver Huff Aaron R Weiskittel Caroline L Noblet David Hiebeler | Published Tuesday, October 13, 2015This theoretical model includes forested polygons and three types of agents: forest landowners, foresters, and peer leaders. Agent rules and characteristics were parameterized from existing literature and an empirical survey of forest landowners.
Peak-seeking Adder
Julia Kasmire Janne M Korhonen | Published Tuesday, December 02, 2014 | Last modified Friday, February 20, 2015Continuing on from the Adder model, this adaptation explores how rationality, learning and uncertainty influence the exploration of complex landscapes representing technological evolution.
The Garbage Can Model of Organizational Choice
Guido Fioretti | Published Saturday, June 22, 2013We reconstruct Cohen, March and Olsen’s Garbage Can model of organizational choice as an agent-based model. We add another means for avoiding making decisions: buck-passing difficult problems to colleagues.
Simulation of the Effects of Disorganization on Goals and Problem Solving
Dinuka Herath | Published Sunday, August 13, 2017 | Last modified Sunday, August 13, 2017This is a model of the occurrence of disorganization and its impact on individual goal setting and problem-solving. This model therefore, explores the effects of disorganization on goal achievement.
Peer reviewed NetLogo model of USA mass shootings
Smarzhevskiy Ivan | Published Tuesday, September 24, 2019 | Last modified Tuesday, April 14, 2020Is the mass shooter a maniac or a relatively normal person in a state of great stress? According to the FBI report (Silver, J., Simons, A., & Craun, S. (2018). A Study of the Pre-Attack Behaviors of Active Shooters in the United States Between 2000 – 2013. Federal Bureau of Investigation, U.S. Department of Justice,Washington, D.C. 20535.), only 25% of the active shooters were known to have been diagnosed by a mental health professional with a mental illness of any kind prior to the offense.
The main objects of the model are the humans and the guns. The main factors influencing behavior are the population size, the number of people with mental disabilities (“psycho” in the model terminology) per 100,000 population, the total number of weapons (“guns”) in the population, the availability of guns for humans, the intensity of stressors affecting humans and the threshold level of stress, upon reaching which a person commits an act of mass shooting.
The key difference (in the model) between a normal person and a psycho is that a psycho accumulates stressors and, upon reaching a threshold level, commits an act of mass shooting. A normal person is exposed to stressors, but reaching the threshold level for killing occurs only when the simultaneous effect of stressors on him exceeds this level.
The population dynamics are determined by the following factors: average (normally distributed) life expectancy (“life_span” attribute of humans) and population growth with the percentage of newborns set by the value of the TickReprRatio% slider of the current population volume from 16 to 45 years old.Thus, one step of model time corresponds to a year.
Peer reviewed SWIRS Spread of a woody invader in riparian systems
Moira Zellner Beatriz Sosa Carlos Andrés Chiale | Published Tuesday, May 09, 2023Riparian forests are one of the most vulnerable ecosystems to the development of biological invasions, therefore limiting their spread is one of the main challenges for conservation. The main factors that explain plant invasions in these ecosystems are the capacity for both short- and long-distance seed dispersion, and the occurrence of suitable habitats that facilitate the establishment of the invasive species. Large floods constitute an abiotic filter for invasion.
This model simulates the spatio-temporal spread of the woody invader Gleditsia. triacanthos in the riparian forest of the National Park Esteros de Farrapos e Islas del Río Uruguay, a riparian system in the coast of the Uruguay river (South America). In this model, we represent different environmental conditions for the development of G. triacanthos, long- and short-distance spread of its fruits, and large floods as the main factor of mortality for fruit and early stages.
Field results show that the distribution pattern of this invasive species is limited by establishment, i.e. it spreads locally through the expansion of small areas, and remotely through new invasion foci. This model recreates this dispersion pattern. We use this model to derive management implications to control the spread of G. triacanthos
This is the final version of the model. To simulate the normative dynamics we used the EmIL (EMergence In the Loop) Framework which was kindly provided by Ulf Lotzmann. http://cfpm.org/EMIL-D5.1.pdf
Interplay between stakeholders of the management of a river
Christophe Sibertin-Blanc Pascal Roggero Bertrand Baldet | Published Wednesday, November 12, 2014This model describes and analyses the outcomes of the confrontation of interests, some conflicting, some common, about the management of a small river in SW France
Individual bias and organizational objectivity
Bo Xu | Published Monday, April 15, 2013 | Last modified Monday, April 08, 2019This model introduces individual bias to the model of exploration and exploitation, simulates knowledge diffusion within organizations, aiming to investigate the effect of individual bias and other related factors on organizational objectivity.
The purpose of the AdaptPumpa model is to analyze the robustness of the Pumpa irrigation system in Nepal to climate change.
Displaying 10 of 71 results for "Emily Silver Huff" clear search