About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 201 results for "Francisco J V%C3%A1zquez" clear search
Simulating the cost of social care in an ageing population
Eric Silverman | Published Thursday, September 16, 2021This model is an agent-based simulation written in Python 2.7, which simulates the cost of social care in an ageing UK population. The simulation incorporates processes of population change which affect the demand for and supply of social care, including health status, partnership formation, fertility and mortality. Fertility and mortality rates are drawn from UK population data, then projected forward to 2050 using the methods developed by Lee and Carter 1992.
The model demonstrates that rising life expectancy combined with lower birthrates leads to growing social care costs across the population. More surprisingly, the model shows that the oft-proposed intervention of raising the retirement age has limited utility; some reductions in costs are attained initially, but these reductions taper off beyond age 70. Subsequent work has enhanced and extended this model by adding more detail to agent behaviours and familial relationships.
The version of the model provided here produces outputs in a format compatible with the GEM-SA uncertainty quantification software by Kennedy and O’Hagan. This allows sensitivity analyses to be performed using Gaussian Process Emulation.
Learning Extension - RAGE RAngeland Grazing Model
Nikita Strelkovskii Cristina I. Apetrei Nikolay Khabarov Valeria Javalera Rincón | Published Saturday, July 22, 2023This is an extension of the original RAGE model (Dressler et al. 2018), where we add learning capabilities to agents, specifically learning-by-doing and social learning (two processes central to adaptive (co-)management).
The extension module is applied to smallholder farmers’ decision-making - here, a pasture (patch) is the private property of the household (agent) placed on it and there is no movement of the households. Households observe the state of the pasture and their neighrbours to make decisions on how many livestock to place on their pasture every year. Three new behavioural types are created (which cannot be combined with the original ones): E-RO (baseline behaviour), E-LBD (learning-by-doing) and E-RO-SL1 (social learning). Similarly to the original model, these three types can be compared regarding long-term social-ecological performance. In addition, a global strategy switching option (corresponding to double-loop learning) allows users to study how behavioural strategies diffuse in a heterogeneous population of learning and non-learning agents.
An important modification of the original model is that extension agents are heterogeneous in how they deal with uncertainty. This is represented by an agent property, called the r-parameter (household-risk-att in the code). The r-parameter is catch-all for various factors that form an agent’s disposition to act in a certain way, such as: uncertainty in the sensing (partial observability of the resource system), noise in the information received, or an inherent characteristic of the agent, for instance, their risk attitude.
Sandy Beach Visitor Flow: An Agent-Based Model
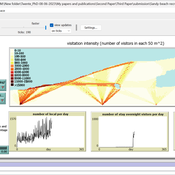
Elham Bakhshianlamouki | Published Thursday, March 14, 2024The model is intended to simulate visitor spatial and temporal dynamics, encompassing their numbers, activities, and distribution along a coastline influenced by beach landscape design. Our primary focus is understanding how the spatial distribution of services and recreational facilities (e.g., beach width, entrance location, recreational facilities, parking availability) impacts visitation density. Our focus is not on tracking the precise visitation density but rather on estimating the areas most affected by visitor activity. This comprehension allows for assessing the diverse influences of beach layouts on spatial visitor density and, consequently, on the landscape’s biophysical characteristics (e.g., vegetation, fauna, and sediment features).
AIforGoodSimulator - Modeling Covid-19 Spread and Potential Interventions in Refugee Camps
Shyaam Ramkumar Woi Sok Oh | Published Thursday, March 18, 2021The Netlogo model is a conceptualization of the Moria refugee camp, capturing the household demographics of refugees in the camp, a theoretical friendship network based on values, and an abstraction of their daily activities. The model then simulates how Covid-19 could spread through the camp if one refugee is exposed to the virus, utilizing transmission probabilities and the stages of disease progression of Covid-19 from susceptible to exposed to asymptomatic / symptomatic to mild / severe to recovered from literature. The model also incorporates various interventions - PPE, lockdown, isolation of symptomatic refugees - to analyze how they could mitigate the spread of the virus through the camp.
Artificial Long House Valley-Black Mesa
Lisa Sattenspiel Amy Warren | Published Thursday, March 19, 2020This model is an extension of the Artificial Long House Valley (ALHV) model developed by the authors (Swedlund et al. 2016; Warren and Sattenspiel 2020). The ALHV model simulates the population dynamics of individuals within the Long House Valley of Arizona from AD 800 to 1350. Individuals are aggregated into households that participate in annual agricultural and demographic cycles. The present version of the model incorporates features of the ALHV model including realistic age-specific fertility and mortality and, in addition, it adds the Black Mesa environment and population, as well as additional methods to allow migration between the two regions.
As is the case for previous versions of the ALHV model as well as the Artificial Anasazi (AA) model from which the ALHV model was derived (Axtell et al. 2002; Janssen 2009), this version makes use of detailed archaeological and paleoenvironmental data from the Long House Valley and the adjacent areas in Arizona. It also uses the same methods as the original AA model to estimate annual maize productivity of various agricultural zones within the Long House Valley. A new environment and associated methods have been developed for Black Mesa. Productivity estimates from both regions are used to determine suitable locations for households and farms during each year of the simulation.
Soy2Grow-ABM-V1
Siavash Farahbakhsh | Published Monday, January 20, 2025The Soy2Grow ABM aims to simulate the adoption of soybean production in Flanders, Belgium. The model primarily considers two types of agents as farmers: 1) arable and 2) dairy farmers. Each farmer, based on its type, assesses the feasibility of adopting soybean cultivation. The feasibility assessment depends on many interrelated factors, including price, production costs, yield, disease, drought (i.e., environmental stress), social pressure, group formations, learning and skills, risk-taking, subsidies, target profit margins, tolerance to bad experiences, etc. Moreover, after adopting soybean production, agents will reassess their performance. If their performance is unsatisfactory, an agent may opt out of soy production. Therefore, one of the main outcomes to look for in the model is the number of adopters over time.
The main agents are farmers. Generally, factors influencing farmers’ decision-making are divided into seven main areas: 1) external environmental factors, 2) cooperation and learning (with slight differences depending on whether they are arable or dairy farmers), 3) crop-specific factors, 4) economics, 5) support frameworks, 6) behavioral factors, and 7) the role of mobile toasters (applicable only to dairy farmers).
Moreover, factors not only influence decision-making but also interact with each other. Specifically, external environmental factors (i.e., stress) will result in lower yield and quality (protein content). The reducing effect, identified during participatory workshops, can reach 50 %. Skills can grow and improve yield; however, their growth has a limit and follows different learning curves depending on how individualistic a farmer is. During participatory workshops, it was identified that, contrary to cooperative farmers, individualistic farmers may learn faster and reach their limits more quickly. Furthermore, subsidies directly affect revenues and profit margins; however, their impact may disappear when they are removed. In the case of dairy farmers, mobile toasters play an important role, adding toasting and processing costs to those producing soy for their animal feed consumption.
Last but not least, behavioral factors directly influence the final adoption decision. For example, high risk-taking farmers may adopt faster, whereas more conservative farmers may wait for their neighbors to adopt first. Farmers may evaluate their success based on their own targets and may also consider other crops rather than soy.
Peer reviewed SIM-VOLATILE: Adoption of emerging circular technologies in the waste-treatment sector
Siavash Farahbakhsh | Published Wednesday, December 14, 2022The SIM-VOLATILE model is a technology adoption model at the population level. The technology, in this model, is called Volatile Fatty Acid Platform (VFAP) and it is in the frame of the circular economy. The technology is considered an emerging technology and it is in the optimization phase. Through the adoption of VFAP, waste-treatment plants will be able to convert organic waste into high-end products rather than focusing on the production of biogas. Moreover, there are three adoption/investment scenarios as the technology enables the production of polyhydroxyalkanoates (PHA), single-cell oils (SCO), and polyunsaturated fatty acids (PUFA). However, due to differences in the processing related to the products, waste-treatment plants need to choose one adoption scenario.
In this simulation, there are several parameters and variables. Agents are heterogeneous waste-treatment plants that face the problem of circular economy technology adoption. Since the technology is emerging, the adoption decision is associated with high risks. In this regard, first, agents evaluate the economic feasibility of the emerging technology for each product (investment scenarios). Second, they will check on the trend of adoption in their social environment (i.e. local pressure for each scenario). Third, they combine these two economic and social assessments with an environmental assessment which is their environmental decision-value (i.e. their status on green technology). This combination gives the agent an overall adaptability fitness value (detailed for each scenario). If this value is above a certain threshold, agents may decide to adopt the emerging technology, which is ultimately depending on their predominant adoption probabilities and market gaps.
MCA-SdA (ABM of mining-community-aquifer interactions in Salar de Atacama, Chile)
Wenjuan Liu | Published Tuesday, December 01, 2020 | Last modified Thursday, November 04, 2021This model represnts an unique human-aquifer interactions model for the Li-extraction in Salar de Atacama, Chile. It describes the local actors’ experience of mining-induced changes in the socio-ecological system, especially on groundwater changes and social stressors. Social interactions are designed specifically according to a long-term local fieldwork by Babidge et al. (2019, 2020). The groundwater system builds on the FlowLogo model by Castilla-Rho et al. (2015), which was then parameterized and calibrated with local hydrogeological inputs in Salar de Atacama, Chile. The social system of the ABM is defined and customozied based on empirical studies to reflect three major stressors: drought stress, population stress, and mining stress. The model reports evolution of groundwater changes and associated social stress dynamics within the modeled time frame.
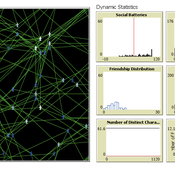
The Friendship Field
Eva Timmer Chrisja van de Kieft | Published Thursday, May 26, 2022 | Last modified Tuesday, August 30, 2022The Friendship Field model aims at modelling friendship formation based on three factors: Extraversion, Resemblance and Status, where social interaction is motivated by the Social Battery. Social Battery is one’s energy and motivation to engage in social contact. Since social contact is crucial for friendship formation, the model included Social Battery to affect social interactions. To our best knowledge, Social Battery is a yet unintroduced concept in research while it is a dynamic factor influencing the social interaction besides one’s characteristics. Extraverts’ Social Batteries charge while interacting and exhaust while being alone. Introverts’ Social Batteries charge while being alone and exhaust while interacting. The aim of the model is to illustrate the concept of Social Battery. Moreover, the Friendship Field shows patterns regarding Extraversion, Resemblance and Status including the mere-exposure effect and friendship by similarity. For the implementation of Status, Kemper’s status-power theory is used. The concept of Social Battery is also linked to Kemper’s theory on the organism as reference group. By running the model for a year (3 interactions moments per day), the friendship dynamics over time can be studied.
We presented the model at the Social Simulation Conference 2022.
Identity and meat eating behaviour
Jiaqi Ge | Published Thursday, September 29, 2022Using data from the British Social Attitude Survey, we develop an agent-based model to study the effect of social influence on the spread of meat-eating behaviour in the British population.
Displaying 10 of 201 results for "Francisco J V%C3%A1zquez" clear search