About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 73 results Diffusion clear search
Agent-based Modelling of Unsustainable and Sustainable Norms Under Resource Constraints
Fachrizal Sinaga Adrian Thomas Sufyan Fawwad | Published Monday, November 24, 2025This model explores the coupled dynamics of social norm diffusion and finite resource depletion. Extending the “Affordance Landscape” framework by Kaaronen & Strelkovskii (2020), this simulation investigates how resource scarcity and regeneration rates influence the adoption of pro-environmental behaviours.
The model addresses the gap by linking behavioural norms to a depleting common-pool resource. It tests whether sustainable norms can diffuse rapidly enough to prevent ecological collapse and identifies “tipping points” where resource scarcity acts as a driver for behavioural change.
Peer reviewed The effect of homophily on co-offending outcomes
Ruslan Klymentiev Christophe Vandeviver Luis E. C. Rocha | Published Friday, September 26, 2025This Agent-Based Model is designed to simulate how similarity-based partner selection (homophily) shapes the formation of co-offending networks and the diffusion of skills within those networks. Its purpose is to isolate and test the effects of offenders’ preference for similar partners on network structure and information flow, under controlled conditions.
In the model, offenders are represented as agents with an individual attribute and a set of skills. At each time step, agents attempt to select partners based on similarity preference. When two agents mutually select each other, they commit a co-offense, forming a tie and exchanging a skill. The model tracks the evolution of network properties (e.g., density, clustering, and tie strength) as well as the spread of skills over time.
This simple and theoretical model does not aim to produce precise empirical predictions but rather to generate insights and test hypotheses about the trade-off between network stability and information diffusion. It provides a flexible framework for exploring how changes in partner selection preferences may lead to differences in criminal network dynamics. Although the model was developed to simulate offenders’ interactions, in principle, it could be applied to other social processes involving social learning and skills exchange.
…
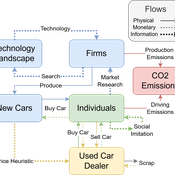
Driving in the wrong direction? A co-evolutionary model of electric vehicle adoption and innovation
Daniel Torren-Peraire | Published Friday, July 11, 2025Car-centric societies face substantial challenges in moving towards sustainable
mobility systems, with internal combustion engine vehicles remaining a major
source of emissions. Electric vehicles play a critical role in addressing this challenge, yet their diffusion depends on the interaction of consumer behaviour, firm
innovation, and policy incentives. This paper develops an agent-based model to
examine these dynamics, calibrated on the data for the state of California over
2001-2023. In the model, heterogeneous car users influenced by their social peers
…
Agent-based Simulation of Innovation Diffusion
Theresa Elbracht | Published Monday, May 19, 2025The agent-based simulation of innovation diffusion is based on the idea of the Bass model (1969).
The adoption of an agent is driven two parameters: its innovativess p and its prospensity to conform with others. The model is designed for a computational experiment building up on the following four model variations:
(i) the agent population it fully connected and all agents share the same parameter values for p and q
(ii) the agent population it fully connected and agents are heterogeneous, i.e. individual parameter values are drawn from a normal distribution
(iii) the agents population is embeded in a social network and all agents share the same parameter values for p and q
…
ABM Code: Locating Cultural Holes Brokers in Diffusion Dynamics across Bright Symbolic Boundaries
Diego Leal | Published Thursday, January 23, 2025The code and data in this repository are associated with the article titled: “Locating Cultural Holes Brokers in Diffusion Dynamics across Bright Symbolic Boundaries.” The NetLogo code (version 6.4.0) is designed to be a standalone piece of code although it uses the ‘nw’ and ‘matrix’ extensions that come integrated with NetLogo 6.4.0. The code was ran on a Windows 10 x 64 machine.
Peer reviewed AgModel
Isaac Ullah | Published Friday, December 06, 2024AgModel is an agent-based model of the forager-farmer transition. The model consists of a single software agent that, conceptually, can be thought of as a single hunter-gather community (i.e., a co-residential group that shares in subsistence activities and decision making). The agent has several characteristics, including a population of human foragers, intrinsic birth and death rates, an annual total energy need, and an available amount of foraging labor. The model assumes a central-place foraging strategy in a fixed territory for a two-resource economy: cereal grains and prey animals. The territory has a fixed number of patches, and a starting number of prey. While the model is not spatially explicit, it does assume some spatiality of resources by including search times.
Demographic and environmental components of the simulation occur and are updated at an annual temporal resolution, but foraging decisions are “event” based so that many such decisions will be made in each year. Thus, each new year, the foraging agent must undertake a series of optimal foraging decisions based on its current knowledge of the availability of cereals and prey animals. Other resources are not accounted for in the model directly, but can be assumed for by adjusting the total number of required annual energy intake that the foraging agent uses to calculate its cereal and prey animal foraging decisions. The agent proceeds to balance the net benefits of the chance of finding, processing, and consuming a prey animal, versus that of finding a cereal patch, and processing and consuming that cereal. These decisions continue until the annual kcal target is reached (balanced on the current human population). If the agent consumes all available resources in a given year, it may “starve”. Starvation will affect birth and death rates, as will foraging success, and so the population will increase or decrease according to a probabilistic function (perturbed by some stochasticity) and the agent’s foraging success or failure. The agent is also constrained by labor caps, set by the modeler at model initialization. If the agent expends its yearly budget of person-hours for hunting or foraging, then the agent can no longer do those activities that year, and it may starve.
Foragers choose to either expend their annual labor budget either hunting prey animals or harvesting cereal patches. If the agent chooses to harvest prey animals, they will expend energy searching for and processing prey animals. prey animals search times are density dependent, and the number of prey animals per encounter and handling times can be altered in the model parameterization (e.g. to increase the payoff per encounter). Prey animal populations are also subject to intrinsic birth and death rates with the addition of additional deaths caused by human predation. A small amount of prey animals may “migrate” into the territory each year. This prevents prey animals populations from complete decimation, but also may be used to model increased distances of logistic mobility (or, perhaps, even residential mobility within a larger territory).
…
Agent-Based Model of Transhumant Decision-Making Processes in Senegal
Cheick Amed Diloma Gabriel TRAORE Etienne DELAY Alassane Bah Djibril Diop | Published Wednesday, July 03, 2024Sahelian transhumance is a type of socio-economic and environmental pastoral mobility. It involves the movement of herds from their terroir of origin (i.e., their original pastures) to one or more host terroirs, followed by a return to the terroir of origin. According to certain pastoralists, the mobility of herds is planned to prevent environmental degradation, given the continuous dependence of these herds on their environment. However, these herds emit Greenhouse Gases (GHGs) in the spaces they traverse. Given that GHGs contribute to global warming, our long-term objective is to quantify the GHGs emitted by Sahelian herds. The determination of these herds’ GHG emissions requires: (1) the artificial replication of the transhumance, and (2) precise knowledge of the space used during their transhumance.
This article presents the design of an artificial replication of the transhumance through an agent-based model named MSTRANS. MSTRANS determines the space used by transhumant herds, based on the decision-making process of Sahelian transhumants.
MSTRANS integrates a constrained multi-objective optimization problem and algorithms into an agent-based model. The constrained multi-objective optimization problem encapsulates the rationality and adaptability of pastoral strategies. Interactions between a transhumant and its socio-economic network are modeled using algorithms, diffusion processes, and within the multi-objective optimization problem. The dynamics of pastoral resources are formalized at various spatio-temporal scales using equations that are integrated into the algorithms.
The results of MSTRANS are validated using GPS data collected from transhumant herds in Senegal. MSTRANS results highlight the relevance of integrated models and constrained multi-objective optimization for modeling and monitoring the movements of transhumant herds in the Sahel. Now specialists in calculating greenhouse gas emissions have a reproducible and reusable tool for determining the space occupied by transhumant herds in a Sahelian country. In addition, decision-makers, pastoralists, veterinarians and traders have a reproducible and reusable tool to help them make environmental and socio-economic decisions.
A Diffusion Study
Diego Leal | Published Sunday, April 21, 2024This ABM
Controlling the misinformation diffusion in social media by the effect of different classes of agents
Ali Khodabandeh Yalabadi | Published Thursday, October 05, 2023An agent-based framework to simulate the diffusion process of a piece of misinformation according to the SBFC model in which the fake news and its debunking compete in a social network. Considering new classes of agents, this model is closer to reality and proposed different strategies how to mitigate and control misinformation.
Influence mining framework for complex networks using igraph
Owais Hussain | Published Monday, September 25, 2023IMine is a flexible framework which can be adopt multiple criteria for convergence to solve Influence Minig problems. It can use any diffusion model, as well as resilience to compute the influence of a set of nodes base on the use case.
The code is written and tested on ‘R’ v3.5
Displaying 10 of 73 results Diffusion clear search