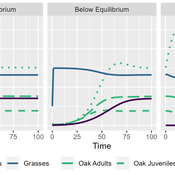
This model is intended to support oak tree management by representing the dynamics of oaks in multiple life stages and their competitors and consumers. This is implemented using a differential equation-based theoretical model representing three life stages of oaks: seedlings, juveniles, and adults. It includes the population dynamics of seedlings transitioning to juveniles, juveniles to adults, and adults producing new seedlings, as well as survival rates for each of the stages. It also includes a model of competition for light and water within seedlings and between seedlings and annual grasses. Finally, there is a predation term representing herbivores eating seedlings and grasses, using a Holling Type II (satiating) response with interference for predators and a death rate which depends on the resource extraction rate.

Resilience of humans in the Upper Paleolithic could provide insights in how to defend against today’s environmental threats. Approximately 13,000 years ago, the Laacher See volcano located in present-day western Germany erupted cataclysmically. Archaeological evidence suggests that this is eruption – potentially against the background of a prolonged cold spell – led to considerable culture change, especially at some distance from the eruption (Riede, 2017). Spatially differentiated and ecologically mediated effects on contemporary social networks as well as social transmission effects mediated by demographic changes in the eruption’s wake have been proposed as factors that together may have led to, in particular, the loss of complex technologies such as the bow-and-arrow (Riede, 2014; Riede, 2009).

This model looks at the impact of the interaction between climate change trajectory and an extreme event, such as the Laacher See eruption, on the generational development of hunter-gatherer bands. Historic data is used to model the distribution and population dynamics of hunter-gatherer bands during these circumstances.

INOvPOP is designed to simulate population dynamics (abundance, sex-age composition and distribution in the landscape) of white-tailed deer (Odocoileus virginianus) for selected Indiana counties.

This work is a java implementation of a study of the viability of a population submitted to floods. The population derives some benefit from living in a certain environment. However, in this environment, floods can occur and cause damage. An individual protection measure can be adopted by those who wish and have the means to do so. The protection measure reduces the damage in case of a flood. However, the effectiveness of this measure deteriorates over time. Individual motivation to adopt this measure is boosted by the occurrence of a flood. Moreover, the public authorities can encourage the population to adopt this measure by carrying out information campaigns, but this comes at a cost. People’s decisions are modelled based on the Protection Motivation Theory (Rogers1975, Rogers 1997, Maddux1983) arguing that the motivation to protect themselves depends on their perception of risk, their capacity to cope with risk and their socio-demographic characteristics.
While the control designing proper informations campaigns to remain viable every time is computed in the work presented in https://www.comses.net/codebases/e5c17b1f-0121-4461-9ae2-919b6fe27cc4/releases/1.0.0/, the aim of the present work is to produce maps of probable viability in case the serie of upcoming floods is unknown as well as much of the parameters for the population dynamics. These maps are bi-dimensional, based on the value of known parameters: the current average wealth of the population and their actual or possible future annual revenues.

A modelling system to simulate Neanderthal demography and distribution in a reconstructed Western Europe for the late Middle Paleolithic.

MOOvPOP is designed to simulate population dynamics (abundance, sex-age composition and distribution in the landscape) of white-tailed deer (Odocoileus virginianus) for a selected sampling region.

Is the mass shooter a maniac or a relatively normal person in a state of great stress? According to the FBI report (Silver, J., Simons, A., & Craun, S. (2018). A Study of the Pre-Attack Behaviors of Active Shooters in the United States Between 2000 – 2013. Federal Bureau of Investigation, U.S. Department of Justice,Washington, D.C. 20535.), only 25% of the active shooters were known to have been diagnosed by a mental health professional with a mental illness of any kind prior to the offense.
The main objects of the model are the humans and the guns. The main factors influencing behavior are the population size, the number of people with mental disabilities (“psycho” in the model terminology) per 100,000 population, the total number of weapons (“guns”) in the population, the availability of guns for humans, the intensity of stressors affecting humans and the threshold level of stress, upon reaching which a person commits an act of mass shooting.
The key difference (in the model) between a normal person and a psycho is that a psycho accumulates stressors and, upon reaching a threshold level, commits an act of mass shooting. A normal person is exposed to stressors, but reaching the threshold level for killing occurs only when the simultaneous effect of stressors on him exceeds this level.
The population dynamics are determined by the following factors: average (normally distributed) life expectancy (“life_span” attribute of humans) and population growth with the percentage of newborns set by the value of the TickReprRatio% slider of the current population volume from 16 to 45 years old.Thus, one step of model time corresponds to a year.

InformalCity, a spatially explicit agent-based model, simulates an artificial city and allows for testing configurations of urban upgrading schemes in informal settlements.

This model is an extension of the Artificial Long House Valley (ALHV) model developed by the authors (Swedlund et al. 2016; Warren and Sattenspiel 2020). The ALHV model simulates the population dynamics of individuals within the Long House Valley of Arizona from AD 800 to 1350. Individuals are aggregated into households that participate in annual agricultural and demographic cycles. The present version of the model incorporates features of the ALHV model including realistic age-specific fertility and mortality and, in addition, it adds the Black Mesa environment and population, as well as additional methods to allow migration between the two regions.

As is the case for previous versions of the ALHV model as well as the Artificial Anasazi (AA) model from which the ALHV model was derived (Axtell et al. 2002; Janssen 2009), this version makes use of detailed archaeological and paleoenvironmental data from the Long House Valley and the adjacent areas in Arizona. It also uses the same methods as the original AA model to estimate annual maize productivity of various agricultural zones within the Long House Valley. A new environment and associated methods have been developed for Black Mesa. Productivity estimates from both regions are used to determine suitable locations for households and farms during each year of the simulation.

This model extends the original Artifical Anasazi (AA) model to include individual agents, who vary in age and sex, and are aggregated into households. This allows more realistic simulations of population dynamics within the Long House Valley of Arizona from AD 800 to 1350 than are possible in the original model. The parts of this model that are directly derived from the AA model are based on Janssen’s 1999 Netlogo implementation of the model; the code for all extensions and adaptations in the model described here (the Artificial Long House Valley (ALHV) model) have been written by the authors. The AA model included only ideal and homogeneous “individuals” who do not participate in the population processes (e.g., birth and death)–these processes were assumed to act on entire households only. The ALHV model incorporates actual individual agents and all demographic processes affect these individuals. Individuals are aggregated into households that participate in annual agricultural and demographic cycles. Thus, the ALHV model is a combination of individual processes (birth and death) and household-level processes (e.g., finding suitable agriculture plots).

As is the case for the AA model, the ALHV model makes use of detailed archaeological and paleoenvironmental data from the Long House Valley and the adjacent areas in Arizona. It also uses the same methods as the original model (from Janssen’s Netlogo implementation) to estimate annual maize productivity of various agricultural zones within the valley. These estimates are used to determine suitable locations for households and farms during each year of the simulation.