About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 118 results for "Brandon Velasco" clear search
Concession Forestry Modeling
Andrew Bell Daniel G Brown Rick L Riolo Jacqueline M Doremus Thomas P Lyon John Vandermeer Arun Agrawal | Published Thursday, January 23, 2014A logging agent builds roads based on the location of high-value hotspots, and cuts trees based on road access. A forest monitor sanctions the logger on observed infractions, reshaping the pattern of road development.
Heterogeneity of preferences and the dynamics of voluntary contributions to public goods
Engi Amin Amal Soliman Mohamed Abouelela | Published Thursday, August 18, 2016 | Last modified Thursday, January 25, 2018This model simulates the heterogeneity of preferences in a PG game and how the interaction between them affects the dynamics of voluntary contributions. Model is based on the results of a human-based experiment.
The Cardial Spread Model
Sean Bergin | Published Friday, September 29, 2017 | Last modified Monday, February 04, 2019The purpose of this model is to provide a platform to test and compare four conceptual models have been proposed to explain the spread of the Impresso-Cardial Neolithic in the west Mediterranean.
Crowdworking Model
Georg Jäger | Published Wednesday, September 25, 2019The purpose of this agent-based model is to compare different variants of crowdworking in a general way, so that the obtained results are independent of specific details of the crowdworking platform. It features many adjustable parameters that can be used to calibrate the model to empirical data, but also when not calibrated it yields essential results about crowdworking in general.
Agents compete for contracts on a virtual crowdworking platform. Each agent is defined by various properties like qualification and income expectation. Agents that are unable to turn a profit have a chance to quit the crowdworking platform and new crowdworkers can replace them. Thus the model has features of an evolutionary process, filtering out the ill suited agents, and generating a realistic distribution of agents from an initially random one. To simulate a stable system, the amount of contracts issued per day can be set constant, as well as the number of crowdworkers. If one is interested in a dynamically changing platform, the simulation can also be initialized in a way that increases or decreases the number of crowdworkers or number of contracts over time. Thus, a large variety of scenarios can be investigated.
An Agent-Based Model of Insurance Customer Behaviour with Word of Mouth Network in C#
Rei England Iqbal Owadally Douglas Wright | Published Friday, March 04, 2022This is an agent-based model with two types of agents: customers and insurers. Insurers are price-takers who choose how much to spend on their service quality, and customers evaluate insurers based on premium, brand preference, and their perceived service quality. Customers are also connected in a small-world network and may share their opinions with their network.
The ABM contains two types of agents: insurers and customers. These act within the environment of a motor insurance market. At each simulation, the model undergoes the following steps:
- Network generation: At the start of the simulation, the model generates a small world network of social links between the customers, and randomly assigns each customer to an initial insurer ...
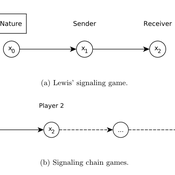
Lewis' Signaling Chains
Giorgio Gosti | Published Wednesday, January 14, 2015 | Last modified Friday, April 03, 2015Signaling chains are a special case of Lewis’ signaling games on networks. In a signaling chain, a sender tries to send a single unit of information to a receiver through a chain of players that do not share a common signaling system.
Peer reviewed Organizational behavior in the hierarchy model
Smarzhevskiy Ivan | Published Tuesday, June 18, 2019 | Last modified Wednesday, July 31, 2019In a two-level hierarchical structure (consisting of the positions of managers and operators), persons holding these positions have a certain performance and the value of their own (personal perception in this, simplified, version of the model) perception of each other. The value of the perception of each other by agents is defined as a random variable that has a normal distribution (distribution parameters are set by the control elements of the interface).
In the world of the model, which is the space of perceptions, agents implement two strategies: rapprochement with agents that perceive positively and distance from agents that perceive negatively (both can be implemented, one of these strategies, or neither, the other strategy, which makes the agent stationary). Strategies are implemented in relation to those agents that are in the radius of perception (PerRadius).
The manager (Head) forms a team of agents. The performance of the group (the sum of the individual productivities of subordinates, weighted by the distance from the leader) varies depending on the position of the agents in space and the values of their individual productivities. Individual productivities, in the current version of the model, are set as a random variable distributed evenly on a numerical segment from 0 to 100. The manager forms the team 1) from agents that are in (organizational) radius (Op_Radius), 2) among agents that the manager perceives positively and / or negatively (both can be implemented, one of the specified rules, or neither, which means the refusal of the command formation).
Agents can (with a certain probability, given by the variable PrbltyOfDecisn%), in case of a negative perception of the manager, leave his group permanently.
It is possible in the model to change on the fly radii values, update the perception value across the entire population and the perception of an individual agent by its neighbors within the perception radius, and the probability values for a subordinate to make a decision about leaving the group.
You can also change the set of strategies for moving agents and strategies for recruiting a team manager. It is possible to add a randomness factor to the movement of agents (Stoch_Motion_Speed, the default is set to 0, that is, there are no random movements).
…
A preliminary extension of the Hemelrijk 1996 model of reciprocal behavior to include feeding
Sean Barton | Published Monday, December 13, 2010 | Last modified Saturday, April 27, 2013A more complete description of the model can be found in Appendix I as an ODD protocol. This model is an expansion of the Hemelrijk (1996) that was expanded to include a simple food seeking behavior.
Demographic microsimulation for individuals and couples
Sabine Zinn | Published Wednesday, January 14, 2015The simulation model conducts fine-grained population projection by specifying life course dynamics of individuals and couples by means of traditional demographic microsimulation and by using agent-based modeling for mate matching.
Agent-based tax evasion model for investigating impacts of public disclosure
Hiroyuki Sano | Published Thursday, March 14, 2024The model explores the impact of public disclosure on tax compliance among diverse agents, including individual taxpayers and a tax authority. It incorporates heterogeneous preferences and income endowments among taxpayers, captured through a utility function that considers psychic costs subtracted from expected pecuniary utility. These costs include moral, reciprocity, and stigma costs associated with norm violations, leading to variations in taxpayers’ risk attitudes and related parameters. The tax authority’s attributes, such as the frequency of random audits, penalty rate, and the choice between partial or full disclosure, remain fixed throughout the simulation. Income endowments and preference parameters are randomly assigned to taxpayers at the outset.
Taxpayers maximize their expected utility by reporting income, taking into account tax, penalty, and audit rates. They make annual decisions based on their own and their peers’ behaviors from the previous year. Taxpayers indirectly interact at the societal level through public disclosure conducted by the tax authority, exchanging tax information among peers. Each period in the simulation collects data on total reported income, average compliance rates per income group, distribution of compliance rates, counts of compliers, full evaders, partial evaders, and the numbers of taxpayers experiencing guilt and anger. The model evaluates whether public disclosure positively or negatively impacts compliance rates and quantifies this impact based on aggregated individual reporting behaviors.
Displaying 10 of 118 results for "Brandon Velasco" clear search