About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 26 results productivity clear search
An agent-based model exploring the biodiversity-agriculture-nutrition dynamics in Eastern Madagascar resulting from alternative land uses
Romain Clercq-Roques Jessica Williams Katja Perez Guzman Marta Kozicka Kristine Belesova Zaid Chalabi | Published Wednesday, July 23, 2025This agent-based model simulates the interactions between smallholder farming households, land-use dynamics, and ecosystem services in a rural landscape of Eastern Madagascar. It explores how alternative agricultural practices —shifting agriculture, rice cultivation, and agroforestry—combined with varying levels of forest protection, influence food production, food security, dietary diversity, and forest biodiversity over time. The landscape is represented as a grid of spatially explicit patches characterized by land use, ecological attributes, and regeneration dynamics. Agents make yearly decisions on land management based on demographic pressures, agricultural returns, and institutional constraints. Crop yields are affected by stochastic biotic and abiotic disruptions, modulated by local ecosystem regulation functions. The model additionally represents foraging as a secondary food source and pressure on biodiversity. The model supports the analysis of long-term trade-offs between agricultural productivity, human nutrition, and conservation under different policy and land-use scenarios.
Peer reviewed Evolution of Conditional Cooperation in a Spatial Public Goods Game
Marco Janssen Francesca Federico Raksha Balakrishna | Published Saturday, March 15, 2025A model to investigate the Evolution of Conditional Cooperation in a Spatial Public Goods Game. We consider two conditional cooperation strategies: one based on thresholds (Battu & Srinivasan, 2020) and another based on independent decisions for each number of cooperating neighbors. We examine the effects of productivity and conditional cooperation criteria on the trajectory of cooperation. Cooperation is evolving with no need for additional mechanisms apart from spatial structure when agents follow conditional strategies. We confirm the positive influence of productivity and cluster formation on the evolution of cooperation in spatial models. Results are robust for the two types of conditional cooperation strategies.
This paper presents an agent-based model to study the dynamics of city-state systems in a constrained environment with limited space and resources. The model comprises three types of agents: city-states, villages, and battalions, where city-states, the primary decision-makers, can build villages for food production and recruit battalions for defense and aggression. In this setting, simulation results, generated through a multi-parameter grid sampling, suggest that risk-seeking strategies are more effective in high-cost scenarios, provided that the production rate is sufficiently high. Also, the model highlights the role of output productivity in defining which strategic preferences are successful in a long-term scenario, with higher outputs supporting more aggressive expansion and military actions, while resource limitations compel more conservative strategies focused on survival and resource conservation. Finally, the results suggest the existence of a non-linear effect of diminishing returns in strategic investments on successful strategies, emphasizing the need for careful resource allocation in a competitive environment.
Peer reviewed COMMONSIM: Simulating the utopia of COMMONISM
Lena Gerdes Manuel Scholz-Wäckerle Ernest Aigner Stefan Meretz Jens Schröter Hanno Pahl Annette Schlemm Simon Sutterlütti | Published Sunday, November 05, 2023This research article presents an agent-based simulation hereinafter called COMMONSIM. It builds on COMMONISM, i.e. a large-scale commons-based vision for a utopian society. In this society, production and distribution of means are not coordinated via markets, exchange, and money, or a central polity, but via bottom-up signalling and polycentric networks, i.e. ex-ante coordination via needs. Heterogeneous agents care for each other in life groups and produce in different groups care, environmental as well as intermediate and final means to satisfy sensual-vital needs. Productive needs decide on the magnitude of activity in groups for a common interest, e.g. the production of means in a multi-sectoral artificial economy. Agents share cultural traits identified by different behaviour: a propensity for egoism, leisure, environmentalism, and productivity. The narrative of this utopian society follows principles of critical psychology and sociology, complexity and evolution, the theory of commons, and critical political economy. The article presents the utopia and an agent-based study of it, with emphasis on culture-dependent allocation mechanisms and their social and economic implications for agents and groups.
Peer reviewed Personnel decisions in the hierarchy
Smarzhevskiy Ivan | Published Friday, August 19, 2022This is a model of organizational behavior in the hierarchy in which personnel decisions are made.
The idea of the model is that the hierarchy, busy with operations, is described by such characteristics as structure (number and interrelation of positions) and material, filling these positions (persons with their individual performance). A particular hierarchy is under certain external pressure (performance level requirement) and is characterized by the internal state of the material (the distribution of the perceptions of others over the ensemble of persons).
The World of the model is a four-level hierarchical structure, consisting of shuff positions of the top manager (zero level of the hierarchy), first-level managers who are subordinate to the top manager, second-level managers (subordinate to the first-level managers) and positions of employees (the third level of the hierarchy). ) subordinated to the second-level managers. Such a hierarchy is a tree, i.e. each position, with the exception of the position of top manager, has a single boss.
Agents in the model are persons occupying the specified positions, the number of persons is set by the slider (HumansQty). Personas have some operational performance (harisma, an unfortunate attribute name left over from the first edition of the model)) and a sense of other personas’ own perceptions. Performance values are distributed over the ensemble of persons according to the normal law with some mean value and variance.
The value of perception by agents of each other is positive or negative (implemented in the model as numerical values equal to +1 and -1). The distribution of perceptions over an ensemble of persons is implemented as a random variable specified by the probability of negative perception, the value of which is set by the control elements of the model interface. The numerical value of the probability equal to 0 corresponds to the case in which all persons positively perceive each other (the numerical value of the random variable is equal to 1, which corresponds to the positive perception of the other person by the individual).
The hierarchy is occupied with operational activity, the degree of intensity of which is set by the external parameter Difficulty. The level of productivity of each manager OAIndex is equal to the level of productivity of the department he leads and is the ratio of the sum of productivity of employees subordinate to the head to the level of complexity of the work Difficulty. An increase in the numerical value of Difficulty leads to a decrease in the OAIndex for all subdivisions of the hierarchy. The managerial meaning of the OAIndex indicator is the percentage of completion of the load specified for the hierarchy as a whole, i.e. the ratio of the actual performance of the structural subdivisions of the hierarchy to the required performance, the level of which is specified by the value of the Difficulty parameter.
…
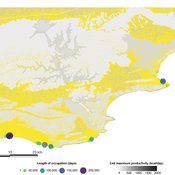
PaleoscapeABM: coastal occupation and shellfish discard
Claudine Gravel-Miguel | Published Tuesday, February 08, 2022This model builds on the Armature distribution within the PaleoscapeABM model, which is itself a variant of the PaleoscapeABM available here written by Wren and Janssen, and.
This model aims to explore where and how much shellfish is discarded at coastal and non-coastal locations by daily coastal foraging. We use this model’s output to test the idea that we can confidently use the archaeological record to evaluate the importance of shellfish in prehistoric people’s diets.
The recognition that aquatic adaptations likely had significant impacts on human evolution triggered an explosion of research on that topic. Recognizing coastal foraging in the past relies on the archaeological signature of that behavior. We use this model to explore why some coastal sites are very intensely occupied and see if it is due to the shellfish productivity of the coast.
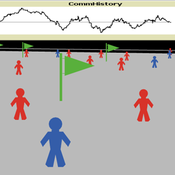
Model of communication between two groups of managers in the course of project implementation
Smarzhevskiy Ivan | Published Monday, December 07, 2020This is a simulation model of communication between two groups of managers in the course of project implementation. The “world” of the model is a space of interaction between project participants, each of which belongs either to a group of work performers or to a group of customers. Information about the progress of the project is publicly available and represents the deviation Earned value (EV) from the planned project value (cost baseline).
The key elements of the model are 1) persons belonging to a group of customers or performers, 2) agents that are communication acts. The life cycle of persons is equal to the time of the simulation experiment, the life cycle of the communication act is 3 periods of model time (for the convenience of visualizing behavior during the experiment). The communication act occurs at a specific point in the model space, the coordinates of which are realized as random variables. During the experiment, persons randomly move in the model space. The communication act involves persons belonging to a group of customers and a group of performers, remote from the place of the communication act at a distance not exceeding the value of the communication radius (MaxCommRadius), while at least one representative from each of the groups must participate in the communication act. If none are found, the communication act is not carried out. The number of potential communication acts per unit of model time is a parameter of the model (CommPerTick).
The managerial sense of the feedback is the stimulating effect of the positive value of the accumulated communication complexity (positive background of the project implementation) on the productivity of the performers. Provided there is favorable communication (“trust”, “mutual understanding”) between the customer and the contractor, it is more likely that project operations will be performed with less lag behind the plan or ahead of it.
The behavior of agents in the world of the model (change of coordinates, visualization of agents’ belonging to a specific communicative act at a given time, etc.) is not informative. Content data are obtained in the form of time series of accumulated communicative complexity, the deviation of the earned value from the planned value, average indicators characterizing communication - the total number of communicative acts and the average number of their participants, etc. These data are displayed on graphs during the simulation experiment.
The control elements of the model allow seven independent values to be varied, which, even with a minimum number of varied values (three: minimum, maximum, optimum), gives 3^7 = 2187 different variants of initial conditions. In this case, the statistical processing of the results requires repeated calculation of the model indicators for each grid node. Thus, the set of varied parameters and the range of their variation is determined by the logic of a particular study and represents a significant narrowing of the full set of initial conditions for which the model allows simulation experiments.
…
Artificial Long House Valley-Black Mesa
Lisa Sattenspiel Amy Warren | Published Thursday, March 19, 2020This model is an extension of the Artificial Long House Valley (ALHV) model developed by the authors (Swedlund et al. 2016; Warren and Sattenspiel 2020). The ALHV model simulates the population dynamics of individuals within the Long House Valley of Arizona from AD 800 to 1350. Individuals are aggregated into households that participate in annual agricultural and demographic cycles. The present version of the model incorporates features of the ALHV model including realistic age-specific fertility and mortality and, in addition, it adds the Black Mesa environment and population, as well as additional methods to allow migration between the two regions.
As is the case for previous versions of the ALHV model as well as the Artificial Anasazi (AA) model from which the ALHV model was derived (Axtell et al. 2002; Janssen 2009), this version makes use of detailed archaeological and paleoenvironmental data from the Long House Valley and the adjacent areas in Arizona. It also uses the same methods as the original AA model to estimate annual maize productivity of various agricultural zones within the Long House Valley. A new environment and associated methods have been developed for Black Mesa. Productivity estimates from both regions are used to determine suitable locations for households and farms during each year of the simulation.
This model extends the original Artifical Anasazi (AA) model to include individual agents, who vary in age and sex, and are aggregated into households. This allows more realistic simulations of population dynamics within the Long House Valley of Arizona from AD 800 to 1350 than are possible in the original model. The parts of this model that are directly derived from the AA model are based on Janssen’s 1999 Netlogo implementation of the model; the code for all extensions and adaptations in the model described here (the Artificial Long House Valley (ALHV) model) have been written by the authors. The AA model included only ideal and homogeneous “individuals” who do not participate in the population processes (e.g., birth and death)–these processes were assumed to act on entire households only. The ALHV model incorporates actual individual agents and all demographic processes affect these individuals. Individuals are aggregated into households that participate in annual agricultural and demographic cycles. Thus, the ALHV model is a combination of individual processes (birth and death) and household-level processes (e.g., finding suitable agriculture plots).
As is the case for the AA model, the ALHV model makes use of detailed archaeological and paleoenvironmental data from the Long House Valley and the adjacent areas in Arizona. It also uses the same methods as the original model (from Janssen’s Netlogo implementation) to estimate annual maize productivity of various agricultural zones within the valley. These estimates are used to determine suitable locations for households and farms during each year of the simulation.
Peer reviewed BAM: The Bottom-up Adaptive Macroeconomics Model
Alejandro Platas López Alejandro Guerra-Hernández | Published Tuesday, January 14, 2020 | Last modified Sunday, July 26, 2020Overview
Purpose
Modeling an economy with stable macro signals, that works as a benchmark for studying the effects of the agent activities, e.g. extortion, at the service of the elaboration of public policies..
…
Displaying 10 of 26 results productivity clear search