The simulation generates two kinds of agents, whose proposals are generated accordingly to their selfish or selfless behaviour. Then, agents compete in order to increase their portfolio playing the ultimatum game with a random-stranger matching.

Juan Castilla-Rho et al. (2015) developed a platform, named FLowLogo, which integrates a 2D, finite-difference solution of the governing equations of groundwater flow with agent-based simulation. We used this model for Rafsanjan Aquifer, which is located in an arid region in Iran. To use FLowLogo for a real case study, one needs to add GIS shapefiles of boundary conditions and modify the code written in NetLogo a little bit. The FlowLogo model used in our research is presented here.

This model simulates the dynamics of agricultural land use change, specifically the transition between agricultural and non-agricultural land use in a spatial context. It explores the influence of various factors such as agricultural profitability, path dependency, and neighborhood effects on land use decisions.

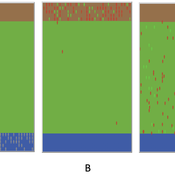
The model operates on a grid of patches representing land parcels. Each patch can be in one of two states: exploited (green, representing agricultural land) or unexploited (brown, representing non-agricultural land). Agents (patches) transition between these states based on probabilistic rules. The main factors affecting these transitions are agricultural profitability, path dependency, and neighborhood effects.
-Agricultural Profitability: This factor is determined by the prob-agri function, which calculates the probability of a non-agricultural patch converting to agricultural based on income differences between agriculture and other sectors. -Path Dependency: Represented by the path-dependency parameter, it influences the likelihood of patches changing their state based on their current state. It’s a measure of inertia or resistance to change. -Neighborhood Effects: The neighborhood function calculates the number of exploited (agricultural) neighbors of a patch. This influences the decision of a patch to convert to agricultural land, representing the influence of surrounding land use on the decision-making process.

Micro-targeted vs stochastic political campaigning agent-based model simulation. Written by Toby D. Pilditch (University of Oxford, University College London), in collaboration with Jens K. Madsen (University of Oxford, London School of Economics)

The purpose of the model is to explore the various impacts on voting intention among a population sample, when both stochastic (traditional) and Micto-targeted campaigns (MTCs) are in play. There are several stages of the model: initialization (setup), campaigning (active running protocols) and vote-casting (end of simulation). The campaigning stage consists of update cycles in which “voters” are targeted and “persuaded” - updating their beliefs in the campaign candidate / policies.

This is an extension of the original RAGE model (Dressler et al. 2018), where we add learning capabilities to agents, specifically learning-by-doing and social learning (two processes central to adaptive (co-)management).

The extension module is applied to smallholder farmers’ decision-making - here, a pasture (patch) is the private property of the household (agent) placed on it and there is no movement of the households. Households observe the state of the pasture and their neighrbours to make decisions on how many livestock to place on their pasture every year. Three new behavioural types are created (which cannot be combined with the original ones): E-RO (baseline behaviour), E-LBD (learning-by-doing) and E-RO-SL1 (social learning). Similarly to the original model, these three types can be compared regarding long-term social-ecological performance. In addition, a global strategy switching option (corresponding to double-loop learning) allows users to study how behavioural strategies diffuse in a heterogeneous population of learning and non-learning agents.

An important modification of the original model is that extension agents are heterogeneous in how they deal with uncertainty. This is represented by an agent property, called the r-parameter (household-risk-att in the code). The r-parameter is catch-all for various factors that form an agent’s disposition to act in a certain way, such as: uncertainty in the sensing (partial observability of the resource system), noise in the information received, or an inherent characteristic of the agent, for instance, their risk attitude.

This model builds on the Armature distribution within the PaleoscapeABM model, which is itself a variant of the PaleoscapeABM available here written by Wren and Janssen, and.

This model aims to explore where and how much shellfish is discarded at coastal and non-coastal locations by daily coastal foraging. We use this model’s output to test the idea that we can confidently use the archaeological record to evaluate the importance of shellfish in prehistoric people’s diets.

The recognition that aquatic adaptations likely had significant impacts on human evolution triggered an explosion of research on that topic. Recognizing coastal foraging in the past relies on the archaeological signature of that behavior. We use this model to explore why some coastal sites are very intensely occupied and see if it is due to the shellfish productivity of the coast.

AgModel is an agent-based model of the forager-farmer transition. The model consists of a single software agent that, conceptually, can be thought of as a single hunter-gather community (i.e., a co-residential group that shares in subsistence activities and decision making). The agent has several characteristics, including a population of human foragers, intrinsic birth and death rates, an annual total energy need, and an available amount of foraging labor. The model assumes a central-place foraging strategy in a fixed territory for a two-resource economy: cereal grains and prey animals. The territory has a fixed number of patches, and a starting number of prey. While the model is not spatially explicit, it does assume some spatiality of resources by including search times.

Demographic and environmental components of the simulation occur and are updated at an annual temporal resolution, but foraging decisions are “event” based so that many such decisions will be made in each year. Thus, each new year, the foraging agent must undertake a series of optimal foraging decisions based on its current knowledge of the availability of cereals and prey animals. Other resources are not accounted for in the model directly, but can be assumed for by adjusting the total number of required annual energy intake that the foraging agent uses to calculate its cereal and prey animal foraging decisions. The agent proceeds to balance the net benefits of the chance of finding, processing, and consuming a prey animal, versus that of finding a cereal patch, and processing and consuming that cereal. These decisions continue until the annual kcal target is reached (balanced on the current human population). If the agent consumes all available resources in a given year, it may “starve”. Starvation will affect birth and death rates, as will foraging success, and so the population will increase or decrease according to a probabilistic function (perturbed by some stochasticity) and the agent’s foraging success or failure. The agent is also constrained by labor caps, set by the modeler at model initialization. If the agent expends its yearly budget of person-hours for hunting or foraging, then the agent can no longer do those activities that year, and it may starve.

Foragers choose to either expend their annual labor budget either hunting prey animals or harvesting cereal patches. If the agent chooses to harvest prey animals, they will expend energy searching for and processing prey animals. prey animals search times are density dependent, and the number of prey animals per encounter and handling times can be altered in the model parameterization (e.g. to increase the payoff per encounter). Prey animal populations are also subject to intrinsic birth and death rates with the addition of additional deaths caused by human predation. A small amount of prey animals may “migrate” into the territory each year. This prevents prey animals populations from complete decimation, but also may be used to model increased distances of logistic mobility (or, perhaps, even residential mobility within a larger territory).

…

Risk assessments are designed to measure cumulative risk and promotive factors for delinquency and recidivism, and are used by criminal and juvenile justice systems to inform sanctions and interventions. Yet, these risk assessments tend to focus on individual risk and often fail to capture each individual’s environmental risk. This agent-based model (ABM) explores the interaction of individual and environmental risk on the youth. The ABM is based on an interactional theory of delinquency and moves beyond more traditional statistical approaches used to study delinquency that tend to rely on point-in-time measures, and to focus on exploring the dynamics and processes that evolve from interactions between agents (i.e., youths) and their environments. Our ABM simulates a youth’s day, where they spend time in schools, their neighborhoods, and families. The youth has proclivities for engaging in prosocial or antisocial behaviors, and their environments have likelihoods of presenting prosocial or antisocial opportunities.

This model was design to test parameters that affects the number of people shot during mass shooting. This basic formulation places a gunman in a crowd and allows the users to manipulate parameters of the gunman.

On July 20th, James Holmes committed a mass shooting in a midnight showing of The Dark Knight Rises. The Aurora Colorado shooting was used as a test case to validate this framework for modeling mass shootings.