About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 1109 results for "Joan A Barcel%C3%B3" clear search
Spread of COVID-19 in University Dormitory Setting
sunnyxjy | Published Sunday, August 16, 2020NetLogo agent-based model to simulate the transmission of COVID-19 in a university dormitory. User can set the number of initial students, buildings, floors, rooms, number of initially infected, and transmission rate. They can also test the effect of masks, sanitizations, elevator allowance, and visits on the effect of the SEIR curve.
Peer reviewed Emergence of Organizations out of Garbage Can Dynamics
Guido Fioretti | Published Monday, April 20, 2020 | Last modified Sunday, April 26, 2020The Garbage Can Model of Organizational Choice (GCM) is a fundamental model of organizational decision-making originally propossed by J.D. Cohen, J.G. March and J.P. Olsen in 1972. In their model, decisions are made out of random meetings of decision-makers, opportunities, solutions and problems within an organization.
With this model, these very same agents are supposed to meet in society at large where they make decisions according to GCM rules. Furthermore, under certain additional conditions decision-makers, opportunities, solutions and problems form stable organizations. In this artificial ecology organizations are born, grow and eventually vanish with time.
Peer reviewed SIM-VOLATILE: Adoption of emerging circular technologies in the waste-treatment sector
Siavash Farahbakhsh | Published Wednesday, December 14, 2022The SIM-VOLATILE model is a technology adoption model at the population level. The technology, in this model, is called Volatile Fatty Acid Platform (VFAP) and it is in the frame of the circular economy. The technology is considered an emerging technology and it is in the optimization phase. Through the adoption of VFAP, waste-treatment plants will be able to convert organic waste into high-end products rather than focusing on the production of biogas. Moreover, there are three adoption/investment scenarios as the technology enables the production of polyhydroxyalkanoates (PHA), single-cell oils (SCO), and polyunsaturated fatty acids (PUFA). However, due to differences in the processing related to the products, waste-treatment plants need to choose one adoption scenario.
In this simulation, there are several parameters and variables. Agents are heterogeneous waste-treatment plants that face the problem of circular economy technology adoption. Since the technology is emerging, the adoption decision is associated with high risks. In this regard, first, agents evaluate the economic feasibility of the emerging technology for each product (investment scenarios). Second, they will check on the trend of adoption in their social environment (i.e. local pressure for each scenario). Third, they combine these two economic and social assessments with an environmental assessment which is their environmental decision-value (i.e. their status on green technology). This combination gives the agent an overall adaptability fitness value (detailed for each scenario). If this value is above a certain threshold, agents may decide to adopt the emerging technology, which is ultimately depending on their predominant adoption probabilities and market gaps.
LAMDA - Learning Agents for Mechanism-Design Analysis
Iris Lorscheid Matthias Meyer | Published Monday, August 08, 2016The simulation model LAMDA investigates the influences of varying cognitive abilities of the decision maker on the truth-inducing effect of the Groves mechanism. Bounded rationality concepts are represented by information states and learning models.
ForagerNet3_Demography_V3
Andrew White | Published Tuesday, November 29, 2016The ForagerNet3_Demography model is a non-spatial ABM designed to serve as a platform for exploring several aspects of hunter-gatherer demography.
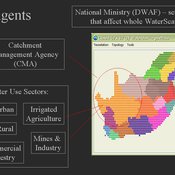
WaterScape
Erin Bohensky | Published Monday, February 06, 2012 | Last modified Saturday, April 27, 2013The WaterScape is an agent-based model of the South African water sector. This version of the model focuses on potential barriers to learning in water management that arise from interactions between human perceptions and social-ecological system conditions.
Hominin Ecodynamics v.1.1 (update for perception and interaction)
C Michael Barton | Published Wednesday, August 15, 2012 | Last modified Saturday, April 27, 2013Models land-use, perception, and biocultural interactions between two forager populations.
Forager mobility and interaction
L S Premo | Published Thursday, January 10, 2013 | Last modified Saturday, April 27, 2013This is a relatively simple foraging-radius model, as described first by Robert Kelly, that allows one to quantify the effect of increased logistical mobility (as represented by increased effective foraging radius, r_e) on the likelihood that 2 randomly placed central place foragers will encounter one another within 5000 time steps.
Opinions on contested energy infrastructures
Annalisa Stefanelli | Published Thursday, June 23, 2016This ABM simulates opinions on a topic (originally contested infrastructures) through the interactions between paired agents and based on the sociopsychological assumptions of social judgment theory (SJT; Sherif & Hovland, 1961).
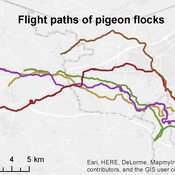
Homing pigeon model
Gudrun Wallentin | Published Saturday, October 29, 2016This model represents the flight paths of a flock of homing pigeons according to their flocking-, orientation- and leadership behaviour.
Displaying 10 of 1109 results for "Joan A Barcel%C3%B3" clear search