About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 4 of 4 results risk-sharing clear search
Risk-Sharing under Heterogeneity: NetLogo simulation
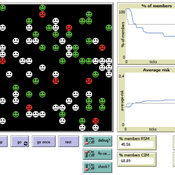
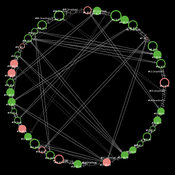
Eva Vriens | Published Monday, February 28, 2022Motivated by the emergence of new Peer-to-Peer insurance organizations that rethink how insurance is organized, we propose a theoretical model of decision-making in risk-sharing arrangements with risk heterogeneity and incomplete information about the risk distribution as core features. For these new, informal organisations, the available institutional solutions to heterogeneity (e.g., mandatory participation or price differentiation) are either impossible or undesirable. Hence, we need to understand the scope conditions under which individuals are motivated to participate in a bottom-up risk-sharing setting. The model puts forward participation as a utility maximizing alternative for agents with higher risk levels, who are more risk averse, are driven more by solidarity motives, and less susceptible to cost fluctuations. This basic micro-level model is used to simulate decision-making for agent populations in a dynamic, interdependent setting. Simulation results show that successful risk-sharing arrangements may work if participants are driven by motivations of solidarity or risk aversion, but this is less likely in populations more heterogeneous in risk, as the individual motivations can less often make up for the larger cost deficiencies. At the same time, more heterogeneous groups deal better with uncertainty and temporary cost fluctuations than more homogeneous populations do. In the latter, cascades following temporary peaks in support requests more often result in complete failure, while under full information about the risk distribution this would not have happened.
RiskNetABM
Birgit Müller Jürgen Groeneveld Karin Frank Meike Will Friederike Lenel | Published Monday, July 20, 2020 | Last modified Monday, May 03, 2021The fight against poverty is an urgent global challenge. Microinsurance is promoted as a valuable instrument for buffering income losses due to health or climate-related risks of low-income households in developing countries. However, apart from direct positive effects they can have unintended side effects when insured households lower their contribution to traditional arrangements where risk is shared through private monetary support.
RiskNetABM is an agent-based model that captures dynamics between income losses, insurance payments and informal risk-sharing. The model explicitly includes decisions about informal transfers. It can be used to assess the impact of insurance products and informal risk-sharing arrangements on the resilience of smallholders. Specifically, it allows to analyze whether and how economic needs (i.e. level of living costs) and characteristics of extreme events (i.e. frequency, intensity and type of shock) influence the ability of insurance and informal risk-sharing to buffer income shocks. Two types of behavior with regard to private monetary transfers are explicitly distinguished: (1) all households provide transfers whenever they can afford it and (2) insured households do not show solidarity with their uninsured peers.
The model is stylized and is not used to analyze a particular case study, but represents conditions from several regions with different risk contexts where informal risk-sharing networks between smallholder farmers are prevalent.
…
Informal risk-sharing cooperatives : ORP and Learning
Juliette Rouchier Victorien Barbet Renaud Bourlès | Published Monday, February 13, 2017 | Last modified Tuesday, May 16, 2023The model studies the dynamics of risk-sharing cooperatives among heterogeneous farmers. Based on their knowledge on their risk exposure and the performance of the cooperative farmers choose whether or not to remain in the risk-sharing agreement.
Hegmon's Model of Sharing
Sean Bergin | Published Thursday, May 02, 2013The purpose of Hegmon’s Sharing model is to develop an understanding of the effect sharing strategies have on household survival.