About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 3 of 3 results imperfect information clear search
An Agent-Based Model of an Insurance Market driven by Supply and Demand with Imperfectly Estimated Strategies in C#
Rei England | Published Sunday, September 24, 2023This is a simulation of an insurance market where the premium moves according to the balance between supply and demand. In this model, insurers set their supply with the aim of maximising their expected utility gain while operating under imperfect information about both customer demand and underlying risk distributions.
There are seven types of insurer strategies. One type follows a rational strategy within the bounds of imperfect information. The other six types also seek to maximise their utility gain, but base their market expectations on a chartist strategy. Under this strategy, market premium is extrapolated from trends based on past insurance prices. This is subdivided according to whether the insurer is trend following or a contrarian (counter-trend), and further depending on whether the trend is estimated from short-term, medium-term, or long-term data.
Customers are modelled as a whole and allocated between insurers according to available supply. Customer demand is calculated according to a logit choice model based on the expected utility gain of purchasing insurance for an average customer versus the expected utility gain of non-purchase.
An Agent-Based Model of an Insurer's Estimated Capital Requirement in a Simple Insurance Market with Imperfect Information in C#
Rei England | Published Sunday, September 24, 2023This is an agent-based model of a simple insurance market with two types of agents: customers and insurers. Insurers set premium quotes for each customer according to an estimation of their underlying risk based on past claims data. Customers either renew existing contracts or else select the cheapest quote from a subset of insurers. Insurers then estimate their resulting capital requirement based on a 99.5% VaR of their aggregate loss distributions. These estimates demonstrate an under-estimation bias due to the winner’s curse effect.
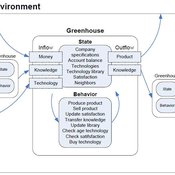
Universal Darwinism in Dutch Greenhouses
Julia Kasmire | Published Wednesday, May 09, 2012 | Last modified Saturday, April 27, 2013An ABM, derived from a case study and a series of surveys with greenhouse growers in the Westland, Netherlands. Experiments using this model showshow that the greenhouse horticulture industry displays diversity, adaptive complexity and an uneven distribution, which all suggest that the industry is an evolving system.