About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 286 results for "Ned Wellman" clear search
Peer reviewed Multilevel Group Selection I
Wayne W. Wakeland Thaddeus Shannon Garry Sotnik | Published Tuesday, April 21, 2020 | Last modified Saturday, July 03, 2021New theoretical agent-based model of population-wide adoption of prosocial common-pool behavior with four parameters (initial percent of adopters, pressure to change behavior, synergy from behavior, and population density); dynamics in behavior, movement, freeriding, and group composition and size; and emergence of multilevel group selection. Theoretical analysis of model’s dynamics identified six regions in model’s parameter space, in which pressure-synergy combinations lead to different outcomes: extinction, persistence, and full adoption. Simulation results verified the theoretical analysis and demonstrated that increases in density reduce number of pressure-synergy combinations leading to population-wide adoption; initial percent of contributors affects underlying behavior and final outcomes, but not size of regions or transition zones between them; and random movement assists adoption of prosocial common-pool behavior.
Peer reviewed Theoretical Model of Oak Persistence Under Competition and Herbivory
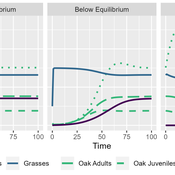
MV Eitzel Solera | Published Tuesday, October 25, 2022This model is intended to support oak tree management by representing the dynamics of oaks in multiple life stages and their competitors and consumers. This is implemented using a differential equation-based theoretical model representing three life stages of oaks: seedlings, juveniles, and adults. It includes the population dynamics of seedlings transitioning to juveniles, juveniles to adults, and adults producing new seedlings, as well as survival rates for each of the stages. It also includes a model of competition for light and water within seedlings and between seedlings and annual grasses. Finally, there is a predation term representing herbivores eating seedlings and grasses, using a Holling Type II (satiating) response with interference for predators and a death rate which depends on the resource extraction rate.
Scientific disagreements and the diagnosticity of evidence
Matteo Michelini | Published Wednesday, December 13, 2023The present model is an abstract ABM designed for theoretical exploration and hypotheses generation. Its main aim is to explore the relationship between disagreement over the diagnostic value of evidence and the formation of polarization in scientific communities.
The model represents a scientific community in which scientists aim to determine whether hypothesis H is true, and we assume that agents are in a world in which H is indeed true. To this end, scientists perform experiments, interpret data and exchange their views on how diagnostic of H the obtained evidence is. Based on how the scientists conduct the inquiry, the community may reach a correct consensus (i.e. a situation in which every scientist agrees that H is correct) or not.
Social and Childcare Provision in Kinship Networks
Umberto Gostoli Eric Silverman | Published Thursday, October 21, 2021This model simulations social and childcare provision in the UK. Agents within simulated households can decide to provide for informal care, or pay for private care, for their loved ones after they have provided for childcare needs. Agents base these decisions on factors including their own health, employment status, financial resources, relationship to the individual in need and geographical location. This model extends our previous simulations of social care by simulating the impact of childcare demand on social care availability within households, which is known to be a significant constraint on informal care provision.
Results show that our model replicates realistic patterns of social and child care provision, suggesting that this framework can be a valuable aid to policy-making in this area.
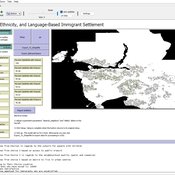
Geospatial Agent-Based Model of Immigrant Settlement Dynamics in Metro Vancouver
Liliana Perez Navid Mahdizadeh Gharakhanlou Maryam Yousefi | Published Wednesday, December 03, 2025This agent-based model simulates how new immigrant households choose where to live in Metro Vancouver under the origins diversity scenario. The model begins with 16,000 household agents, reflecting an expected annual population increase of about 42,500 people based on an average household size of 2.56. Each agent is assigned four characteristics: one of ten origin categories, income level (adjusted using NOC data and recent immigrant earnings), likelihood of having children, and preferred mode of commuting. The ten origin groups are drawn from Census patterns, including six subgroups within the broader Asian category (China, India, the Philippines, Iran, South Korea, and Other Asian countries) and two categories for immigrants from the Americas. This refined classification better captures the diversity of newcomers arriving in the region.
A Model of Iterated Ultimatum game
Andrea Scalco | Published Tuesday, February 24, 2015 | Last modified Monday, March 09, 2015The simulation generates two kinds of agents, whose proposals are generated accordingly to their selfish or selfless behaviour. Then, agents compete in order to increase their portfolio playing the ultimatum game with a random-stranger matching.
The Targeted Subsidies Plan Model
Hassan Bashiri | Published Thursday, September 21, 2023The targeted subsidies plan model is based on the economic concept of targeted subsidies.
The targeted subsidies plan model simulates the distribution of subsidies among households in a community over several years. The model assumes that the government allocates a fixed amount of money each year for the purpose of distributing cash subsidies to eligible households. The eligible households are identified by dividing families into 10 groups based on their income, property, and wealth. The subsidy is distributed to the first four groups, with the first group receiving the highest subsidy amount. The model simulates the impact of the subsidy distribution process on the income and property of households in the community over time.
The model simulates a community of 230 households, each with a household income and wealth that follows a power-law distribution. The number of household members is modeled by a normal distribution. The model allocates a fixed amount of money each year for the purpose of distributing cash subsidies among eligible households. The eligible households are identified by dividing families into 10 groups based on their income, property, and wealth. The subsidy is distributed to the first four groups, with the first group receiving the highest subsidy amount.
The model runs for a period of 10 years, with the subsidy distribution process occurring every month. The subsidy received by each household is assumed to be spent, and a small portion may be saved and added to the household’s property. At the end of each year, the grouping of households based on income and assets is redone, and a number of families may be moved from one group to another based on changes in their income and property.
…
Modeling The Transition to Public School Choice (Model II from paper)
Spiro Maroulis Eytan Bakshy Louis Gomez Uri Wilensky | Published Friday, March 22, 2013 | Last modified Tuesday, August 27, 2013This is an agent-based model that captures the dynamic processes related to moving from an educational system where the school a student attends is based on assignment to a neighborhood school, to one that gives households more choice among existing and newly formed public schools.
AMBAWA, an Agent-based Model of Biomass flows in Agropastoral areas of West Africa
Christophe Le Page Tidiane Diarisso Nadine Andrieu Marc Corbeels François Bousquet Pablo Tittonell David Berre | Published Monday, November 23, 2015 | Last modified Sunday, April 12, 2020AMBAWA simulates the flows of biomass between crop and livestock systems at the field, farm, and village scales in order to showcase innovating management practices of soil fertility in West Africa.
Peer reviewed Emergent Firms Model
J M Applegate | Published Friday, July 13, 2018The Emergent Firm (EF) model is based on the premise that firms arise out of individuals choosing to work together to advantage themselves of the benefits of returns-to-scale and coordination. The Emergent Firm (EF) model is a new implementation and extension of Rob Axtell’s Endogenous Dynamics of Multi-Agent Firms model. Like the Axtell model, the EF model describes how economies, composed of firms, form and evolve out of the utility maximizing activity on the part of individual agents. The EF model includes a cash-in-advance constraint on agents changing employment, as well as a universal credit-creating lender to explore how costs and access to capital affect the emergent economy and its macroeconomic characteristics such as firm size distributions, wealth, debt, wages and productivity.
Displaying 10 of 286 results for "Ned Wellman" clear search