About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 2 of 2 results vertical transmission clear search
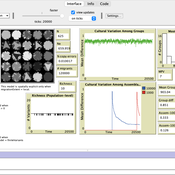
Cultural transmission in structured populations
Luke Premo | Published Wednesday, November 13, 2024This structured population model is built to address how migration (or intergroup cultural transmission), copying error, and time-averaging affect regional variation in a single selectively neutral discrete cultural trait under different mechanisms of cultural transmission. The model allows one to quantify cultural differentiation between groups within a structured population (at equilibrium) as well as between regional assemblages of time-averaged archaeological material at two different temporal scales (1,000 and 10,000 ticks). The archaeological assemblages begin to accumulate only after a “burn-in” period of 10,000 ticks. The model includes two different representations of copying error: the infinite variants model of copying error and the finite model of copying error. The model also allows the user to set the variant ceiling value for the trait in the case of the finite model of copying error.
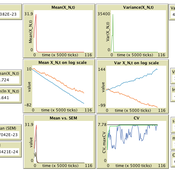
Population size limits the coefficient of variation in continuous traits affected by proportional copying error
Luke Premo | Published Thursday, June 18, 2020This version of the accumulated copying error (ACE) model is designed to address the following research question: how does finite population size (N) affect the coefficient of variation (CV) of a continuous cultural trait under the assumptions that the only source of copying error is visual perception error and that the continuous trait can take any positive value (i.e., it has no upper bound)? The model allows one to address this question while assuming the continuous trait is transmitted via vertical transmission, unbiased transmission, prestige biased transmission, mean conformist transmission, or median conformist transmission. By varying the parameter, p, one can also investigate the effect of population size under a mix of vertical and non-vertical transmission, whereby on average (1-p)N individuals learn via vertical transmission and pN individuals learn via either unbiased transmission, prestige biased transmission, mean conformist transmission, or median conformist transmission.