About the CoMSES Model Library more info
Our mission is to help computational modelers at all levels engage in the establishment and adoption of community standards and good practices for developing and sharing computational models. Model authors can freely publish their model source code in the Computational Model Library alongside narrative documentation, open science metadata, and other emerging open science norms that facilitate software citation, reproducibility, interoperability, and reuse. Model authors can also request peer review of their computational models to receive a DOI.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with additional detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 3 of 3 results behavioral economic clear
Peer reviewed Neighbor Influenced Energy Retrofit (NIER) agent-based model
Eric Boria | Published Friday, April 03, 2020The NIER model is intended to add qualitative variables of building owner types and peer group scales to existing energy efficiency retrofit adoption models. The model was developed through a combined methodology with qualitative research, which included interviews with key stakeholders in Cleveland, Ohio and Detroit and Grand Rapids, Michigan. The concepts that the NIER model adds to traditional economic feasibility studies of energy retrofit decision-making are differences in building owner types (reflecting strategies for managing buildings) and peer group scale (neighborhoods of various sizes and large-scale Districts). Insights from the NIER model include: large peer group comparisons can quickly raise the average energy efficiency values of Leader and Conformist building owner types, but leave Stigma-avoider owner types as unmotivated to retrofit; policy interventions such as upgrading buildings to energy-related codes at the point of sale can motivate retrofits among the lowest efficient buildings, which are predominantly represented by the Stigma-avoider type of owner; small neighborhood peer groups can successfully amplify normal retrofit incentives.
An Agent-Based Simulation of Continuous-Time Public Goods Games
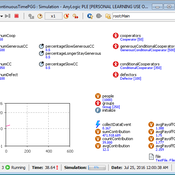
Tuong Vu | Published Thursday, May 17, 2018 | Last modified Tuesday, April 02, 2019To our knowledge, this is the first agent-based simulation of continuous-time PGGs (where participants can change contributions at any time) which are much harder to realise within both laboratory and simulation environments.
Work related to this simulation has been published in the following journal article:
Vu, Tuong Manh, Wagner, Christian and Siebers, Peer-Olaf (2019) ‘ABOOMS: Overcoming the Hurdles of Continuous-Time Public Goods Games with a Simulation-Based Approach’ Journal of Artificial Societies and Social Simulation 22 (2) 7 http://jasss.soc.surrey.ac.uk/22/2/7.html. doi: 10.18564/jasss.3995
Abstract:
…
Generic servicising model (SPREE project)
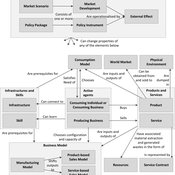
Reinier Van Der Veen Kasper H Kisjes Igor Nikolic | Published Wednesday, August 26, 2015 | Last modified Wednesday, September 28, 2016This generic agent-based model allows the user to simulate and explore the influence of servicising policies on the uptake of servicising and on economic, environmental and social effects, notably absolute decoupling.