(De-)Stabilising effect of diffusions 1.0.0
Diffusions or transitions are typically seen as unstable because they are thought to be periods of large, obvious and coordinated change that shifts the system from one equilibrium to the other.
However, Prigogine (a Nobel prize winner) suggests that diffusions are actually stabilizing forces. While the dynamic equilibria appear stable, they contain constant, low level, change that is hard to see because it is uncoordinated.
The difference between the dynamic equilibria and diffusions/transitions may not be the amount of change, but the uniformity of change. This would suggest that neither is inherently more or less stable, which runs counter to the way people usually think about the various states.
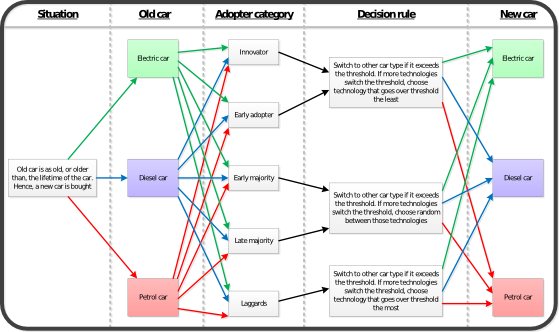
The model represents a complex, communicating network in which agents represent vehicle owners. Each owner purchases new vehicles when the current vehicle expires on the basis of their adopter characteristics, their past history of vehicle purchases, the vehicles they observe among their neighbours, and the available vehicle options. The model output includes the number of agents that own each vehicle type at each time step. This output can be sorted by vehicle type, chopped into strings, and then compressed into ZIP files. The ZIP file sizes can be used to approximate the stability of the system as captured by that vehicle type at that time, so comparing ZIP file sizes provides some insight onto system stability.